iwbe.ru → English writers

Steps to determine the horizontal asymptote. How to find the asymptotes of a graph of a function? How many asymptotes can a graph of a function have?

Asymptote of the graph of a function y \u003d f (x) is called a line that has the property that the distance from the point (x, f (x)) to this line tends to zero with an unlimited removal of the graph point from the origin.

Figure 3.10. graphical examples are given vertical, horizontal And oblique asymptote.

Finding the asymptotes of the graph is based on the following three theorems.

The vertical asymptote theorem. Let the function y \u003d f (x) be defined in some neighborhood of the point x 0 (possibly excluding this point itself) and at least one of the one-sided limits of the function be equal to infinity, i.e. Then the line x \u003d x 0 is the vertical asymptote of the graph of the function y \u003d f (x).

Obviously, the line x \u003d x 0 cannot be a vertical asymptote if the function is continuous at the point x 0, since in this case . Therefore, vertical asymptotes should be sought at the discontinuity points of a function or at the ends of its domain.

Theorem on the horizontal asymptote. Let the function y \u003d f (x) be defined for sufficiently large x and there be a finite limit of the function . Then the line y = b is the horizontal asymptote of the graph of the function.

Comment. If only one of the limits is finite, then the function has, respectively, left-sided or right-sided horizontal asymptote.

In the event that , the function may have an oblique asymptote.

Oblique asymptote theorem. Let the function y = f(x) be defined for sufficiently large x and there be finite limits . Then the line y = kx + b is an oblique asymptote of the graph of the function.

Without proof.

The oblique asymptote, as well as the horizontal one, can be right-handed or left-handed if the basis of the corresponding limits is infinity of a certain sign.

The study of functions and the construction of their graphs usually includes the following steps:

1. Find the domain of the function.

2. Investigate the function for even-odd.

3. Find the vertical asymptotes by examining the discontinuity points and the behavior of the function on the boundaries of the domain of definition, if they are finite.

4. Find horizontal or oblique asymptotes by examining the behavior of the function at infinity.

5. Find extrema and intervals of monotonicity of the function.

6. Find the convexity intervals of the function and the inflection points.

7. Find points of intersection with the coordinate axes and, possibly, some additional points that refine the graph.

Function differential

It can be proved that if a function has a limit for some base equal to final number, then it can be represented as the sum of this number and an infinitesimal value with the same base (and vice versa): .

Let's apply this theorem to a differentiable function: .

Thus, the increment of the function Dy consists of two terms: 1) linear with respect to Dx, i.e. f`(x)Dx; 2) non-linear with respect to Dx, i.e. a(Dx)Dx. At the same time, since , this second term is an infinitesimal of a higher order than Dx (as Dx tends to zero, it tends to zero even faster).

Differential function is called the main, linear with respect to Dx part of the increment of the function, equal to the product incremental derivative of the independent variable dy = f `(x)Dх.

Find the differential of the function y = x.

Since dy = f `(x)Dx = x`Dx = Dx, then dx = Dx, i.e. the differential of an independent variable is equal to the increment of this variable.

Therefore, the formula for the differential of a function can be written as dy = f `(x)dх. That is why one of the symbols for the derivative is the fraction dy/dх.

The geometric meaning of the differential is illustrated
figure 3.11. Take an arbitrary point M(x, y) on the graph of the function y = f(x). Let's give the argument x an increment Dx. Then the function y = f(x) will receive an increment Dy = f(x + Dх) - f(x). Let's draw a tangent to the graph of the function at the point M, which forms an angle a with the positive direction of the x-axis, i.e. f `(x) = tg a. From right triangle MKN
KN \u003d MN * tg a \u003d Dx * tg a \u003d f `(x) Dx \u003d dy.

Thus, the differential of a function is the increment in the ordinate of the tangent drawn to the graph of the function at a given point when x is incremented by Dx.

The properties of a differential are basically the same as those of a derivative:

3. d(u ± v) = du ± dv.

4. d(uv) = v du + u dv.

5. d(u/v) = (v du - u dv)/v 2 .

However, there is an important property of the differential of a function that its derivative does not have - this is differential form invariance.

From the definition of the differential for the function y = f(x), the differential is dy = f`(x)dх. If this function y is complex, i.e. y = f(u), where u = j(x), then y = f and f `(x) = f `(u)*u`. Then dy = f`(u)*u`dx. But for the function
u = j(x) differential du = u`dx. Hence dy = f `(u)*du.

Comparing the equalities dy = f `(x)dх and dy = f `(u)*du, we make sure that the differential formula does not change if instead of a function of the independent variable x we consider a function of the dependent variable u. This property of the differential is called the invariance (i.e., invariance) of the form (or formula) of the differential.

However, there is still a difference in these two formulas: in the first of them, the differential of the independent variable is equal to the increment of this variable, i.e. dx = Dx, and in the second, the differential of the function du is only the linear part of the increment of this function Du, and only for small Dх du » Du.

The concept of asymptotes

One of milestones plotting functions is to find asymptotes. We met with asymptotes more than once: when plotting functions , y=tgx, y=ctgx. We have defined them as lines that the graph of a function “tends for” but never crosses. It's time to give a precise definition of asymptotes.

There are three types of asymptotes: vertical, horizontal, and oblique. In the drawing, the asymptotes are usually denoted by dotted lines.

Consider the following artificially plotted function graph (Fig. 16.1), on the example of which all types of asymptotes are clearly visible:

We give a definition for each type of asymptote:

1. Direct x=a called vertical asymptote functions if .

2. Direct y=s called horizontal asymptote functions if .

3. Direct y=kx+b called oblique asymptote functions if .

Geometrically, the definition of an oblique asymptote means that as →∞ the graph of a function approaches a straight line arbitrarily close y=kx+b, i.e. they are practically the same. The difference is practically identical expressions tends to zero.

Note that the horizontal and oblique asymptotes are considered only under the condition →∞. Sometimes they are distinguished into horizontal and oblique asymptotes as →+∞ and →-∞.

Asymptote Search Algorithm

The following algorithm can be used to find asymptotes:

There may be one vertical asymptote, several or none at all.

If c is a number, then y=s is the horizontal asymptote;
If c is infinity, then there are no horizontal asymptotes.

If a function is a ratio of two polynomials, then if the function has horizontal asymptotes, we will not look for oblique asymptotes - they do not exist.

Consider examples of finding asymptotes of a function:

Example 16.1. Find the asymptotes of the curve.

Solution X-1≠0; X≠1.

Let's check if the line is x= 1 vertical asymptote. To do this, we calculate the limit of the function at the point x= 1: .

x= 1 - vertical asymptote.

With= .

With= = . Because With=2 (number), then y=2 is the horizontal asymptote.

Since the function is a ratio of polynomials, in the presence of horizontal asymptotes we assert that there are no oblique asymptotes.

x= 1 and the horizontal asymptote y=2. For clarity, the graph of this function is shown in Fig. 16.2.

Example 16.2. Find the asymptotes of the curve.

Solution. 1. Find the domain of the function: X-2≠0; X≠2.

Let's check if the line is x= 2 vertical asymptote. To do this, we calculate the limit of the function at the point x= 2: .

We got that, therefore, x= 2 - vertical asymptote.

2. To search for horizontal asymptotes, we find: With= .

Since there is an uncertainty in the limit, we use the L'Hopital rule: With= = . Because With is infinity, then there are no horizontal asymptotes.

3. To search for oblique asymptotes, we find:

We got an uncertainty of the form , we use the L'Hopital rule: = =1. b according to the formula: .

b= = =

Got that b= 2. Then y=kx+b – oblique asymptote. In our case, it looks like: y=x+2.

Rice. 16.3

Thus, this function has a vertical asymptote x= 2 and oblique asymptote y=x+2. For clarity, the graph of the function is shown in Fig. 16.3.

Control questions:

Lecture 17

In this lecture, we will summarize all the previously studied material. The ultimate goal of our long journey is to be able to investigate any analytically given function and build its graph. Important parts of our study will be the study of the function for extrema, the determination of intervals of monotonicity, convexity and concavity of the graph, the search for inflection points, asymptotes of the graph of the function.

Taking into account all the above aspects, we present scheme for studying the function and plotting .

1. Find the domain of the function.

2. Investigate the function for even-odd:

if , then the function is even (the graph of an even function is symmetrical with respect to the axis OU);

if , then the function is odd (the graph of an odd function is symmetrical with respect to the origin);

Otherwise, the function is neither even nor odd.

3. Investigate the function for periodicity (among the functions we study, only trigonometric functions can be periodic).

4. Find the points of intersection of the graph of the function with the coordinate axes:

· Oh: at=0 (we solve the equation only if we can use the methods known to us);

· OU: X=0.

5. Find the first derivative of the function and critical points of the first kind.

6. Find monotonicity intervals and extrema of the function.

7. Find the second derivative of the function and critical points of the second kind.

8. Find the intervals of convexity-concavity of the function graph and inflection points.

9. Find the asymptotes of the graph of the function.

10. Graph the function. When building, consider cases of possible location of the graph near the asymptotes :

11. If necessary, select control points for more accurate construction.

Consider a scheme for studying a function and plotting its graph using specific examples:

Example 17.1. Plot the function .

Solution. 1. This function defined on the entire number line except for X=3, because at this point the denominator goes to zero.

2. To determine the evenness and oddness of the function, we find:

We see that and , therefore, the function is neither even nor odd.

3. The function is non-periodic.

4. Find the points of intersection with the coordinate axes. To find the point of intersection with the axis Oh accept at=0. We get the equation: . So, the point (0; 0) is the point of intersection with the coordinate axes.

5. Find the derivative of the function according to the rule of differentiation of a fraction: = = = = .

To find the critical points, we find the points at which the derivative of the function is equal to 0 or does not exist.

If =0, therefore, . The product is then 0 when at least one of the factors is 0: or .

X-3) 2 is equal to 0, i.e. does not exist at X=3.

So, the function has three critical points of the first kind: ; ; .

6. On the real axis, we mark the critical points of the first kind, and mark the point with a punctured dot, because it does not define a function.

Arrange the signs of the derivative = on each interval:

t.min

t.max

On intervals where , the original function increases (at (-∞;0] ), where - decreases (at ).

Dot X=0 is the maximum point of the function. To find the maximum of the function, let's find the value of the function at the point 0: .

Dot X=6 is the minimum point of the function. To find the minimum of the function, let's find the value of the function at point 6: .

The results of the research can be entered in the table. The number of rows in the table is fixed and equal to four, and the number of columns depends on the function under study. In the cells of the first row, the intervals into which the critical points divide the domain of the function definition are sequentially entered, including the critical points themselves. In order to avoid errors when constructing points that do not belong to the definition area, it is possible not to include them in the table.

The second row of the table contains the signs of the derivative on each of the considered intervals and the value of the derivative at the critical points. In accordance with the signs of the derivative of the function, the intervals of increase, decrease, and extrema of the function are marked in the third line.

The last line is used to denote the maximum and minimum of the function.

X	(-∞;0)		(0;3)	(3;6)		(6;+ ∞)
	+		-	-		+
f(x)
conclusions		max			min

7. Find the second derivative of the function as a derivative of the first derivative: = =

Take out in the numerator X-3 outside the brackets and do the reduction:

We present in the numerator like terms: .

Let us find critical points of the second kind: points at which the second derivative of the function is equal to zero or does not exist.

0 if =0. This fraction cannot be equal to zero, therefore, there are no points at which the second derivative of the function is equal to zero.

Does not exist if the denominator ( X-3) 3 is 0, i.e. does not exist at X=3. :Oh , OU, origin, units of measure for each axis.

Before plotting a function, you need to:

draw asymptotes with dotted lines;

mark the points of intersection with the coordinate axes;

Rice. 17.1

mark the maximum and minimum of the function, and it is recommended to designate the maximum and minimum of the function directly on the drawing with arcs: k or ;

· Using the obtained data on the intervals of increase, decrease, convexity and concavity, construct a graph of the function. The branches of the graph should "tend" to the asymptotes, but not cross them.

Check whether the graph of the function corresponds to the study: if the function is even or odd, then whether the symmetry is observed; whether the theoretically found intervals of increase and decrease, convexity and concavity, inflection points.

11. For more precise construction, you can select multiple control points. For example, let's find the function values at points -2 and 7:

We adjust the graph taking into account the control points.

Control questions:

What is the algorithm for plotting a function graph?
Can a function have an extremum at points that do not belong to the domain of definition?

CHAPTER 3. 3. INTEGRAL CALCULUS OF THE FUNCTION

Asymptotes of the graph of a function

The ghost of the asymptote has been wandering around the site for a long time in order to finally materialize in a single article and bring special delight to readers puzzled full function study. Finding the asymptotes of the graph is one of the few parts of the specified task, which is covered in school course only in an overview, since events revolve around the calculation function limits, but they still belong to higher mathematics. Visitors who are poorly versed in mathematical analysis, I think the hint is understandable ;-) ... stop-stop, where are you going? limits- it's easy!

Examples of asymptotes met immediately in the first lesson about graphs of elementary functions, and now the topic is receiving detailed consideration.

So what is an asymptote?

Imagine variable point, which "travels" along the graph of the function. The asymptote is straight, to whcih unlimited close the graph of the function approaches as its variable point goes to infinity.

Note : the definition is meaningful, if you need a formulation in the notation of mathematical analysis, please refer to the textbook.

On a plane, asymptotes are classified according to their natural arrangement:

1) Vertical asymptotes, which are given by an equation of the form , where "alpha" - real number. The popular representative defines the y-axis itself,
with an attack of mild nausea, we recall hyperbole.

2) Oblique asymptotes traditionally written straight line equation with a slope factor. Sometimes a special case is singled out as a separate group - horizontal asymptotes. For example, the same hyperbola with asymptote .

Quickly off we go, let's hit the topic with a short automatic burst:

How many asymptotes can a graph of a function have?

None, one, two, three... or an infinite number. We will not go far for examples, we will remember elementary functions. Parabola, cubic parabola, sinusoid have no asymptotes at all. The graph of an exponential, logarithmic function has a single asymptote. The arctangent, arccotangent has two of them, and the tangent, cotangent has an infinite number. It is not uncommon for a graph to have both horizontal and vertical asymptotes. Hyperbole, will always love you.

What means ?

Vertical asymptotes of a graph of a function

The vertical asymptote of a graph is usually at the point of infinity functions. It's simple: if at a point the function suffers an infinite break, then the straight line given by the equation is the vertical asymptote of the graph.

Note : note that the notation is used to denote two perfect different concepts. The point is implied or the equation of a straight line - depends on the context.

Thus, to establish the presence of a vertical asymptote at a point, it suffices to show that at least one from unilateral limits endless. Most often this is the point where the denominator of the function zero. In fact, we have already found vertical asymptotes in the last examples of the lesson. on the continuity of the function. But in some cases there is only one one-sided limit, and if it is infinite, then again - love and favor the vertical asymptote. The simplest illustration: and the y-axis (see. Graphs and properties of elementary functions).

From the above, the obvious fact also follows: if the function is continuous on, then there are no vertical asymptotes. For some reason, a parabola came to mind. Indeed, where can you “stick” a straight line here? ... yes ... I understand ... the followers of Uncle Freud huddled in hysterics =)

The converse statement is generally not true: for example, the function is not defined on the entire real line, but it is completely deprived of asymptotes.

Oblique asymptotes of a graph of a function

Oblique (as a special case - horizontal) asymptotes can be drawn if the function argument tends to "plus infinity" or "minus infinity". That's why the graph of a function cannot have more than two oblique asymptotes. For example, the graph of an exponential function has a single horizontal asymptote at , and the graph of the arc tangent at has two such asymptotes, and different ones.

When the graph here and there approaches the only oblique asymptote, then it is customary to unite “infinities” under a single entry. For example, ... you guessed it right: .

General rule of thumb:

If there are two final limit , then the straight line is the oblique asymptote of the graph of the function at . If at least one of the above limits is infinite, then there is no oblique asymptote.

Note : the formulas remain valid if "x" tends only to "plus infinity" or only to "minus infinity".

Let us show that the parabola has no oblique asymptotes:

The limit is infinite, so there is no oblique asymptote. Note that in finding the limit no longer needed because the answer has already been received.

Note : if you have (or will have) difficulty understanding the plus-minus, minus-plus signs, please see the help at the beginning of the lesson
about infinitesimal functions, where I told how to correctly interpret these signs.

It is obvious that any quadratic, cubic function, polynomial of the 4th and higher degrees also does not have oblique asymptotes.

And now let's make sure that at the graph also does not have an oblique asymptote. To uncover uncertainty, we use L'Hopital's rule:
, which was to be verified.

When the function grows indefinitely, however, there is no such straight line to which its graph would approach infinitely close.

Let's move on to the practical part of the lesson:

How to find the asymptotes of a graph of a function?

This is how a typical task is formulated, and it involves finding ALL asymptotes of the graph (vertical, oblique / horizontal). Although, to be more precise in the formulation of the question, we are talking about a study for the presence of asymptotes (after all, there may not be any at all). Let's start with something simple:

Example 1

Find asymptotes of the graph of a function

Solution It is convenient to break it into two points:

1) First we check if there are vertical asymptotes. The denominator vanishes at , and it is immediately clear that at this point the function suffers endless gap, and the straight line given by the equation is the vertical asymptote of the graph of the function . But before drawing such a conclusion, it is necessary to find one-sided limits:

I remind you of the calculation technique, which I likewise dwelled on in the article Function continuity. break points. In the expression under the limit sign, instead of "x" we substitute . There is nothing interesting in the numerator:
.

But in the denominator it turns out infinitesimal a negative number :
, it determines the fate of the limit.

The left-hand limit is infinite, and, in principle, it is already possible to pass a verdict on the presence of a vertical asymptote. But one-sided limits are needed not only for this - they HELP TO UNDERSTAND, HOW the graph of the function is located and plot it CORRECTLY. Therefore, we must also calculate the right-hand limit:

Conclusion: one-sided limits are infinite, which means that the line is a vertical asymptote of the graph of the function at .

First limit finite, which means that it is necessary to “continue the conversation” and find the second limit:

The second limit too finite.

So our asymptote is:

Conclusion: the straight line given by the equation is the horizontal asymptote of the graph of the function at .

To find the horizontal asymptote
You can use the simplified formula:

If exists finite limit , then the line is the horizontal asymptote of the graph of the function at .

It is easy to see that the numerator and denominator of the function one order of growth, which means that the desired limit will be finite:

Answer:

According to the condition, it is not necessary to complete the drawing, but if in full swing function research, then on the draft we immediately make a sketch:

Based on the three limits found, try to independently figure out how the graph of the function can be located. Quite difficult? Find 5-6-7-8 points and mark them on the drawing. However, the graph of this function is constructed using transformations of the elementary function graph, and readers who have carefully examined Example 21 of this article will easily guess what kind of curve it is.

Example 2

Find asymptotes of the graph of a function

This is an example for independent solution. The process, I remind you, is conveniently divided into two points - vertical asymptotes and oblique asymptotes. In the sample solution, the horizontal asymptote is found using a simplified scheme.

In practice, fractional-rational functions are most often encountered, and after training on hyperbolas, we will complicate the task:

Example 3

Find asymptotes of the graph of a function

Solution: One, two and done:

1) The vertical asymptotes are found at the points of infinite discontinuity, so you need to check if the denominator goes to zero. We will decide quadratic equation:

The discriminant is positive, so the equation has two real roots, and work is added significantly =)

In order to further find one-sided limits, it is convenient to factorize the square trinomial:
(for compact notation, "minus" was introduced in the first bracket). For safety net, we will perform a check, mentally or on a draft, opening the brackets.

Let's rewrite the function in the form

Find one-sided limits at the point :

And at the point:

Thus, the straight lines are the vertical asymptotes of the graph of the function under consideration.

2) If you look at the function , then it is quite obvious that the limit will be finite and we have a horizontal asymptote. Let's show it in a short way:

Thus, the straight line (abscissa) is the horizontal asymptote of the graph of this function.

Answer:

The found limits and asymptotes give a lot of information about the graph of the function. Try to mentally imagine the drawing, taking into account the following facts:

Sketch your version of the graph on a draft.

Of course, the limits found do not unequivocally determine the type of graph, and you may make a mistake, but the exercise itself will be of invaluable help during full function study. The correct picture is at the end of the lesson.

Example 4

Find asymptotes of the graph of a function

Example 5

Find asymptotes of the graph of a function

These are tasks for independent decision. Both graphs again have horizontal asymptotes, which are immediately detected by the following features: in Example 4 order of growth denominator more than the order of growth of the numerator, and in Example 5 the numerator and denominator one order of growth. In the sample solution, the first function is investigated for the presence of oblique asymptotes in a full way, and the second - through the limit .

Horizontal asymptotes, in my subjective impression, are noticeably more common than those that are "truly tilted". Long awaited general case:

Example 6

Find asymptotes of the graph of a function

Solution: classics of the genre:

1) Since the denominator is positive, the function continuous on the entire number line, and there are no vertical asymptotes. …Is it good? Not the right word - great! Item #1 is closed.

2) Check the presence of oblique asymptotes:

First limit finite, so let's move on. During the calculation of the second limit to eliminate uncertainty "infinity minus infinity" we bring the expression to a common denominator: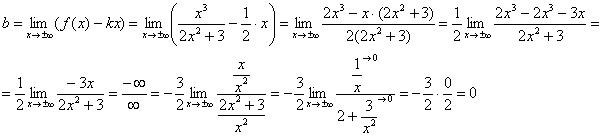

The second limit too finite, therefore, the graph of the function under consideration has an oblique asymptote:

Conclusion:

Thus, for the graph of the function infinitely close approaches a straight line:

Note that it intersects its oblique asymptote at the origin, and such intersection points are quite acceptable - it is important that "everything is normal" at infinity (actually, we are talking about asymptotes exactly there).

Example 7

Find asymptotes of the graph of a function

Solution: there is nothing much to comment on, so I will draw up an approximate sample of a final solution:

1) Vertical asymptotes. Let's explore the point.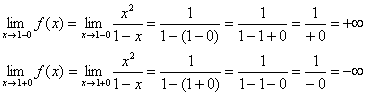

The straight line is the vertical asymptote for the plot at .

2) Oblique asymptotes:

The straight line is the oblique asymptote for the graph at .

Answer:

The found one-sided limits and asymptotes allow us to assume with high certainty what the graph of this function looks like. Correct drawing at the end of the lesson.

Example 8

Find asymptotes of the graph of a function

This is an example for an independent solution, for the convenience of calculating some limits, you can divide the numerator by the denominator term by term. And again, analyzing the results, try to draw a graph of this function.

Obviously, the owners of the "real" oblique asymptotes are the graphs of those fractional-rational functions for which the highest degree of the numerator one more the highest degree of the denominator. If more, there will be no oblique asymptote (for example, ).

But other miracles happen in life:

Example 9

Example 11

Examine the graph of a function for asymptotes

Solution: it's obvious that , therefore, we consider only the right half-plane, where there is a graph of the function.

Thus, the straight line (y-axis) is the vertical asymptote for the graph of the function at .

2) The study of the oblique asymptote can be carried out according to the full scheme, but in the article Rules of L'Hospital we found out that linear function higher order of growth than logarithmic, therefore: (see example 1 of the same lesson).

Conclusion: the abscissa axis is the horizontal asymptote of the graph of the function at .

Answer:
, If ;
, If .

Drawing for clarity:

Interestingly, a seemingly similar function has no asymptotes at all (those who wish can check this).

Two final self-study examples:

Example 12

Examine the graph of a function for asymptotes

If the distance d from a point of the curve y \u003d f (x), which has an infinite branch, to some definite straight line tends to zero as the point moves along this curve to infinity, then the straight line is called the asymptote of the curve.

There are asymptotes: 1) horizontal, 2) vertical and 3) oblique.

1. The curve y \u003d f (x) has a horizontal asymptote y \u003d b only if there is a finite limit of the function f (x) at , and this limit is equal to b, i.e. if

2. The curve y \u003d f (x) has a vertical asymptote x \u003d a, if at . To determine the vertical asymptotes, it is necessary to find those values of the argument near which f(x) increases in absolute value without limit. If such values of the argument are a1, a2, ..., then the equations of vertical asymptotes will be

x \u003d a1, x \u003d a2 ...

3. To determine the oblique asymptote y \u003d kx + b of the curve y \u003d f (x), you need to find the numbers k and b from the formulas

(cases should be considered separately). Oblique asymptotes for the curve y = f(x) exist if and only if these limits are finite. When determining these limits, it is convenient to use L'Hospital's rule.

Example. Find curve asymptotes

Solution. There are no horizontal asymptotes. We find the vertical asymptote from the condition

2x + 3 = 0 => x = - 3/2, while y
, When
, y
, When
. We define oblique asymptotes, the equation of which has the form: y = kx + b

Since k and b have finite values and are equal to each other at x
and at x
, then there is a unique oblique asymptote whose equation

General Function Study

A complete study of a function is usually understood as the solution of such questions:

Determining the scope of a function.

Revealing the question of even and odd functions.

Definition of function break points.

Determining the asymptotes of the graph of a function.

Definition of intervals of increase and decrease of function.

Determining the extremum of a function.

Determining the intervals of convexity and concavity of the function graph.

Definition of inflection points.

Finding the intersection with the coordinate axes.

Plotting a function.

Example. Exploring the function

D(y)=(
). The function is continuous on the entire domain of definition. There are no break points.

The function is neither even, odd, or periodic.

There are no break points.

There are no vertical asymptotes;
, there are no oblique asymptotes.

5, 6.
. Critical points x = -2, x = 0.

	( )		( )
Sign		= 0
Function Behavior	Increasing	3	Increasing

7, 8.
,
at x = 1,
does not exist for x = 0.

	( )				( )
Sign		=		= 0
Function Behavior	Convex top	Not an inflection point	Convex top	inflection point	convex down

9.
x=0 and x=-5.

Exercise 1

Calculate the determinant of the matrix A of the second order

Calculate the determinant of the matrix B of the third order

Calculate the determinant of matrix B by expanding it in any row and any column

Calculate the determinant of the matrix B, using the properties of the determinants. Reduce the calculation of the third order determinant to the calculation of one second order determinant

Option 1

Option 2

Option 3

Option 4

Option 5

Option 6

Option 7

Option 8



Option 9



Option 10

Task 2

1. Solve the system of equations using Cramer's method Ah = a

Solve the system of equations by Cramer's method INx = b

Solve the system of equations using the Gauss method INx = b

Task 3.

Ah = a

Solve the system of equations by the matrix method INx = b

Task 4.

Calculate the rank of a matrix.

1., 2.
;

3.
4.

5.
6.

7.
8

9.
10.

Task 5

Given two vertices of a triangle Δ ABC: A (X 1 ,y 1 ), IN(X 2 ,y 2 ) and dot D (x 3 , y 3 ) intersections of heights:

a) make an equation of heights, medians, bisectors of a triangle Δ ABC.

b) find the equations of the lines passing through the vertices of the triangle and parallel to the sides.

c) determine the lengths of the heights of the triangle and the distance from the point M (X 4 , y 4 ) to the sides of the triangle.

x 1	y 1	x 2	y 2	x 3	y 3	x 4	y 4

Task 6.

Given the coordinates of the vertices of the pyramid ABCD: A (X 1 ,y 1 , z 1 ), IN(X 2 ,y 2 , z 3 ) ,C (x 2 , y 2 , z 2 ) ,D (X 4 , y 4 , z 3 )

1) rib length AB;.

2) angle between ribs AB And AD;

3) angle between edge AD and edge ABC;

4) face area ABC;

5) the volume of the pyramid;

6) equation of a straight line AB;

7) plane equation ABC;

8) the equation of the height lowered from the top D to the brink ABC.

x 1

y 1

z 1

x 2

y 2

z 2

x 3

y 3

z 3

x 4

y 4

z 4

Task 7.

Task 8. Find the domain of the function

10.

Task 9. Graph the function

10.

Task 10. Find the limits of the function

1.a)
, b)
, V)
,

G)
, e)

2.a)
, b)
, V)
,

G)
, e)

3.a)
, b)
, V)
,

G)
, e)

4. a)
, b)
, V)
,

G)
, e)

5.a)
, b)
, V)
,

G)
, e)

6.a)
, b)
, V)
,

G)
, e)

7. a)
, b)
, V)
,

G)
, e)

8.a)
, b)
, V)
,

G)
, e)

9.a)
, b)
, V)
,

G)
, e)

10.a)
, b)
, V)
,

G)
, e)

Task 11. Find the derivative

1.
, b),

V)
, G)
, e)
, e)

2. a)
, b)
, V)
,

G)
, e)
,e)

3. a), b)
, V)
, G)
, e)
, e)

4. a)
, b)
, V)
,

G)
, e)
, e)

5. a)
, b)
, V)
, G)
, e)
,

6. a)
, b)
, V)
, G)
, e)
,

7. a)
, b),

V)
, G)
, e)
,

8. a)
, b)
, V)
, G)
, e)
,

9. a)
, b)
, V)
,

G)
, e)
, e)

10. a)
, b)
, V)
,

G)
, e)
, e)

Task 12. Show that the function satisfies the equality

Task 13. Find the second derivative of a function given parametrically.

1 .
6.

2.
7

3.
8

4.
9.

5.
10.

Task 14. Find limits using L'Hospital's rule

Task 15. Find the extrema of the given functions.

1.
6.

2.
7.

3.
8.

4.
9.

5.
10.

Task 16. Find the largest and smallest value on the specified segments and at the specified intervals.

Task 17. Conduct a complete study of these functions and draw their graphs.

1.
6.

2.
7.

3.
8.

4.
9.

5.
10.

Literature:

Bavrin I.I. Course of higher mathematics.-M.: Enlightenment, 1992.-400 p.

Bronstein I.N., Semendyaev K.A. Handbook of mathematics. M, 1967, 608 s

General course of higher mathematics for economists, edited by V.I. Ermakov-M. "Infra-M". 1999 - 655 p.

Teush V.L. Course of higher mathematics. - M.: Soviet science, 1958, 270 p.

Shipachev V.S. Higher Mathematics: Tutorial M. Higher school, 1990.-479s.

Higher Mathematics for Economists: Textbook for High Schools / N.Sh. Kremer, B.A. Putko and others; M: UNITI, 2002. - 461 p.

Val'ev K.G., Dzhalladova I.A. Helper.

The solution can be conveniently broken down into two parts:

1) First we check if there are vertical asymptotes. The denominator vanishes at, and it is immediately clear that at this point the function suffers an infinite discontinuity, and the straight line given by the equation is the vertical asymptote of the function graph. But before drawing such a conclusion, it is necessary to find one-sided limits:

I remind you of the calculation technique, which I similarly discussed in the article Continuity of a function. Break points. In the expression under the sign of the limit, instead of "x" we substitute. There is nothing interesting in the numerator:

But in the denominator, an infinitely small negative number is obtained:

It determines the fate of the limit.

The left-hand limit is infinite, and, in principle, it is already possible to pass a verdict on the presence of a vertical asymptote. But one-sided limits are needed not only for this - they HELP YOU UNDERSTAND HOW the graph of the function is located and build it CORRECTLY. Therefore, we must also calculate the right-hand limit:

Conclusion: one-sided limits are infinite, which means that the straight line is a vertical asymptote of the graph of the function at.

The first limit is finite, which means that it is necessary to “continue the conversation” and find the second limit:

The second limit is also finite.

So our asymptote is:

Conclusion: the straight line given by the equation is the horizontal asymptote of the graph of the function at.

To find the horizontal asymptote, you can use a simplified formula:

If there is a finite limit, then the line is a horizontal asymptote of the graph of the function at.

It is easy to see that the numerator and denominator of the function are of the same order of growth, which means that the desired limit will be finite:

According to the condition, it is not necessary to complete the drawing, but if the study of the function is in full swing, then we immediately make a sketch on the draft:

Based on the three limits found, try to independently figure out how the graph of the function can be located. Quite difficult? Find 5-6-7-8 points and mark them on the drawing. However, the graph of this function is built using transformations of the graph of an elementary function, and readers who have carefully examined Example 21 of this article will easily guess what kind of curve it is.

This is a do-it-yourself example. The process, I remind you, is conveniently divided into two points - vertical asymptotes and oblique asymptotes. In the sample solution, the horizontal asymptote is found using a simplified scheme.

In practice, fractional-rational functions are most often encountered, and after training on hyperbolas, we will complicate the task:

Find asymptotes of the graph of a function

Solution: One, two and done:

1) The vertical asymptotes are at points of infinite discontinuity, so we need to check if the denominator vanishes. We will decide quadratic equation:

The discriminant is positive, so the equation has two real roots and there is a lot of work added

In order to further find one-sided limits, it is convenient to factorize the square trinomial:

(for compact notation, "minus" was introduced in the first bracket). For safety net, we will perform a check, mentally or on a draft, opening the brackets.

Let's rewrite the function in the form

Find one-sided limits at a point:

asymptote graph function limit

And at the point:

Thus, the straight lines are the vertical asymptotes of the graph of the function under consideration.

2) If you look at the function, it is quite obvious that the limit will be finite and we have a horizontal asymptote. Let's show it in a short way:

Thus, the straight line (abscissa) is the horizontal asymptote of the graph of this function.

The found limits and asymptotes give a lot of information about the graph of the function. Try to mentally imagine the drawing, taking into account the following facts:

Sketch your version of the graph on a draft.

Of course, the found limits do not unambiguously determine the type of graph, and you may make a mistake, but the exercise itself will be of invaluable help in the course of a complete study of the function. The correct picture is at the end of the lesson.

Find asymptotes of the graph of a function

These are tasks for independent decision. Both graphs again have horizontal asymptotes, which are immediately detected by the following features: in Example 4, the denominator increases in order of magnitude greater than the numerator, and in Example 5, the numerator and denominator are of the same order of growth. In the sample solution, the first function is investigated for the presence of oblique asymptotes in a full way, and the second - through the limit.

Horizontal asymptotes, in my subjective impression, are noticeably more common than those that are "truly tilted". Long awaited general case:

Find asymptotes of the graph of a function

Solution: classic of the genre:

1) Since the denominator is positive, the function is continuous on the entire number line, and there are no vertical asymptotes. …Is it good? Not the right word - great! Item #1 is closed.
2) Check the presence of oblique asymptotes:

The second limit is also finite, therefore, the graph of the function under consideration has an oblique asymptote:

Thus, at , the graph of the function is infinitely close to a straight line.

Find asymptotes of the graph of a function

Solution: there is nothing much to comment on, so I will draw up an approximate sample of a final solution:

1) Vertical asymptotes. Let's explore the point.

The straight line is the vertical asymptote for the plot at.

2) Oblique asymptotes:

The straight line is the oblique asymptote for the plot at.

The found one-sided limits and asymptotes allow us to assume with high certainty what the graph of this function looks like.

Find asymptotes of the graph of a function

Obviously, the owners of "real" oblique asymptotes are the graphs of those fractional-rational functions whose highest degree of the numerator is one greater than the highest degree of the denominator. If more - there will be no oblique asymptote (for example,).

But other miracles also happen in life.

Steps to determine the horizontal asymptote. How to find the asymptotes of a graph of a function? How many asymptotes can a graph of a function have?

Asymptotes of the graph of a function

So what is an asymptote?

How many asymptotes can a graph of a function have?

What means ?

Vertical asymptotes of a graph of a function

Oblique asymptotes of a graph of a function

How to find the asymptotes of a graph of a function?

To find the horizontal asymptoteYou can use the simplified formula:

General Function Study

To find the horizontal asymptote
You can use the simplified formula: