Passaggi per determinare l'asintoto orizzontale. Come trovare gli asintoti di un grafico di una funzione? Quanti asintoti può avere il grafico di una funzione?
Asintoto del grafico di una funzione y \u003d f (x) è chiamata una linea che ha la proprietà che la distanza dal punto (x, f (x)) a questa linea tende a zero con una rimozione illimitata del punto del grafico dall'origine.
Figura 3.10. vengono forniti esempi grafici verticale, orizzontale E obliquo asintoto.
Trovare gli asintoti del grafico si basa sui seguenti tre teoremi.
Il teorema dell'asintoto verticale. Lascia che la funzione y \u003d f (x) sia definita in qualche intorno del punto x 0 (possibilmente escludendo questo punto stesso) e almeno uno dei limiti unilaterali della funzione sia uguale a infinito, cioè Quindi la linea x \u003d x 0 è l'asintoto verticale del grafico della funzione y \u003d f (x).
Ovviamente la linea x \u003d x 0 non può essere un asintoto verticale se la funzione è continua nel punto x 0, poiché in questo caso 
. Pertanto gli asintoti verticali vanno ricercati nei punti di discontinuità di una funzione o agli estremi del suo dominio.
Teorema sull'asintoto orizzontale. Lascia che la funzione y \u003d f (x) sia definita per x sufficientemente grande e che ci sia un limite finito della funzione . Allora la linea y = b è l'asintoto orizzontale del grafico della funzione.
Commento. Se solo uno dei limiti è finito, allora la funzione ha, rispettivamente, lato sinistro O lato destro asintoto orizzontale.
Nel caso in cui , la funzione può avere un asintoto obliquo.
Teorema dell'asintoto obliquo. Sia definita la funzione y = f(x) per x sufficientemente grande e vi siano limiti finiti 
. Allora la retta y = kx + b è un asintoto obliquo del grafico della funzione.
Senza prove.
L'asintoto obliquo, così come quello orizzontale, può essere destrorso o mancino se la base dei limiti corrispondenti è l'infinito di un certo segno.
Lo studio delle funzioni e la costruzione dei loro grafici prevede solitamente i seguenti passaggi:
1. Trova il dominio della funzione.
2. Esaminare la funzione per pari-dispari.
3. Trovare gli asintoti verticali esaminando i punti di discontinuità e il comportamento della funzione sui confini del dominio di definizione, se sono finiti.
4. Trova gli asintoti orizzontali o obliqui esaminando il comportamento della funzione all'infinito.
5. Trova gli estremi e gli intervalli di monotonia della funzione.
6. Trova gli intervalli di convessità della funzione e i punti di flesso.
7. Trova i punti di intersezione con gli assi delle coordinate ed, eventualmente, alcuni punti aggiuntivi che affinano il grafico.
Differenziale di funzione
Si può dimostrare che se una funzione ha limite per qualche base uguale a numero finale, allora può essere rappresentato come la somma di questo numero e di un valore infinitesimo con la stessa base (e viceversa): .
Applichiamo questo teorema ad una funzione differenziabile: .
Pertanto l’incremento della funzione Dy è composto da due termini: 1) lineare rispetto a Dx, cioè f`(x)Dx; 2) non lineare rispetto a Dx, ovvero a(Dx)Dx. Allo stesso tempo, da allora 
, questo secondo termine è un infinitesimo di ordine superiore a Dx (poiché Dx tende a zero, tende a zero anche più velocemente).
Differenziale La funzione è detta parte principale della funzione incremento, lineare rispetto a Dx, pari al prodotto della derivata e dell'incremento della variabile indipendente dy = f `(x)Dx.
Trova il differenziale della funzione y = x.
Poiché dy = f `(x)Dx = x`Dx = Dx, allora dx = Dx, cioè il differenziale di una variabile indipendente è uguale all'incremento di quella variabile.
Pertanto, la formula per il differenziale di una funzione può essere scritta come dy = f `(x)dх. Ecco perché uno dei simboli della derivata è la frazione dy/dх.
Viene illustrato il significato geometrico del differenziale
figura 3.11. Prendi un punto arbitrario M(x, y) sul grafico della funzione y = f(x). Diamo all'argomento x un incremento Dx. Allora la funzione y = f(x) riceverà un incremento Dy = f(x + Dх) - f(x). Disegniamo una tangente al grafico della funzione nel punto M, che forma un angolo a con la direzione positiva dell'asse x, cioè f`(x) = tg a. Da triangolo rettangolo MKN
KN \u003d MN * tg a \u003d Dx * tg a \u003d f `(x) Dx \u003d dy.
Pertanto, il differenziale di una funzione è l'incremento nell'ordinata della tangente tracciata sul grafico della funzione in un dato punto quando x viene incrementato di Dx.
Le proprietà di un differenziale sono sostanzialmente le stesse di un derivato:
3. d(u±v) = du±dv.
4. d(uv) = v du + u dv.
5. d(u/v) = (v du - u dv)/v 2 .
Tuttavia, esiste un'importante proprietà del differenziale di una funzione che la sua derivata non ha: questa è invarianza della forma differenziale.
Dalla definizione del differenziale per la funzione y = f(x), il differenziale è dy = f`(x)dх. Se questa funzione y è complessa, cioè y = f(u), dove u = j(x), quindi y = f e f `(x) = f `(u)*u`. Allora dy = f`(u)*u`dx. Ma per la funzione
u = j(x) differenziale du = u`dx. Quindi dy = f `(u)*du.
Confrontando le uguaglianze dy = f `(x)dх e dy = f `(u)*du, ci assicuriamo che la formula differenziale non cambia se invece di una funzione della variabile indipendente x consideriamo una funzione della variabile dipendente u. Questa proprietà del differenziale è chiamata invarianza (cioè invarianza) della forma (o formula) del differenziale.
Tuttavia, c'è ancora una differenza tra queste due formule: nella prima il differenziale della variabile indipendente è uguale all'incremento di questa variabile, cioè dx = Dx, e nel secondo, il differenziale della funzione du è solo la parte lineare dell'incremento di questa funzione Du, e solo per piccoli Dх du » Du.
- Il concetto di asintoti
Uno di pietre miliari tracciare le funzioni è trovare asintoti. Abbiamo incontrato gli asintoti più di una volta: quando si tracciano le funzioni, y=tgx, y=ctgx. Le abbiamo definite come linee verso le quali il grafico di una funzione “tende” ma non oltrepassa mai. E' giunto il momento di dare una definizione precisa di asintoti.
Esistono tre tipi di asintoti: verticale, orizzontale e obliquo. Nel disegno gli asintoti sono solitamente indicati con linee tratteggiate.
Considera il seguente grafico della funzione tracciato artificialmente (Fig. 16.1), sull'esempio del quale sono chiaramente visibili tutti i tipi di asintoti:
Diamo una definizione per ogni tipo di asintoto:
1. Diretto x=a chiamato asintoto verticale funziona se .
2. Diretto y=s chiamato asintoto orizzontale funziona se .
3. Diretto y=kx+b chiamato asintoto obliquo funziona se .
Dal punto di vista geometrico, la definizione di asintoto obliquo significa che quanto →∞ il grafico di una funzione si avvicina ad una retta arbitrariamente vicina y=kx+b, cioè. sono praticamente uguali. La differenza è praticamente espressioni identiche tende a zero.
Si noti che gli asintoti orizzontale e obliquo sono considerati solo nella condizione →∞. A volte si distinguono in asintoti orizzontali e obliqui come →+∞ e →-∞.
- Algoritmo di ricerca degli asintoti
Per trovare gli asintoti è possibile utilizzare il seguente algoritmo:
Potrebbe esserci un asintoto verticale, diversi o nessuno.
- Se c è un numero, allora y=sè l'asintoto orizzontale;
- Se c è infinito, allora non ci sono asintoti orizzontali.
Se una funzione è un rapporto di due polinomi, allora se la funzione ha asintoti orizzontali, non cercheremo asintoti obliqui: non esistono.
Considera esempi di ricerca di asintoti di una funzione:
Esempio 16.1. Trova gli asintoti della curva.
Soluzione X-1≠0; X≠1.
Controlliamo se la linea lo è x= 1 asintoto verticale. Per fare ciò, calcoliamo il limite della funzione nel punto x= 1: .
x= 1 - asintoto verticale.
Con= .
Con= = . Perché Con=2 (numero), quindi y=2è l'asintoto orizzontale.
Poiché la funzione è un rapporto di polinomi, in presenza di asintoti orizzontali affermiamo che non esistono asintoti obliqui.
x= 1 e l'asintoto orizzontale y=2. Per chiarezza, il grafico di questa funzione è mostrato in Fig. 16.2.
Esempio 16.2. Trova gli asintoti della curva.
Soluzione. 1. Trova il dominio della funzione: X-2≠0; X≠2.
Controlliamo se la linea lo è x= 2 asintoto verticale. Per fare ciò, calcoliamo il limite della funzione nel punto x= 2: .
Abbiamo capito, quindi x= 2 - asintoto verticale.
2. Per cercare gli asintoti orizzontali, troviamo: Con= .
Poiché c'è un'incertezza nel limite, utilizziamo la regola di L'Hopital: Con= = . Perché Conè infinito, allora non ci sono asintoti orizzontali.
3. Per cercare gli asintoti obliqui, troviamo:
Ottenuta un'incertezza della forma, usiamo la regola di L'Hopital: = =1. B secondo la formula: .
b= = =
Capito b= 2. Quindi y=kx+b – asintoto obliquo. Nel nostro caso, sembra: y=x+2.
|
Domande di controllo:
Lezione 17
In questa lezione riassumeremo tutto il materiale precedentemente studiato. L'obiettivo finale del nostro lungo viaggio è essere in grado di indagare qualsiasi funzione data analiticamente e costruire il suo grafico. Parti importanti del nostro studio saranno lo studio della funzione per estremi, la determinazione degli intervalli di monotonicità, convessità e concavità del grafico, la ricerca dei punti di flesso, degli asintoti del grafico della funzione.
Tenendo conto di tutti gli aspetti di cui sopra, presentiamo schema per lo studio della funzione e il grafico .
1. Trova il dominio della funzione.
2. Esamina la funzione per pari-dispari:
se , allora la funzione è pari (il grafico di una funzione pari è simmetrico rispetto all'asse UO);
se , allora la funzione è dispari (il grafico di una funzione dispari è simmetrico rispetto all'origine);
Altrimenti la funzione non è né pari né dispari.
3. Studiare la funzione per la periodicità (tra le funzioni che studiamo, solo le funzioni trigonometriche possono essere periodiche).
4. Trova i punti di intersezione del grafico della funzione con gli assi delle coordinate:
· OH: A=0 (risolviamo l'equazione solo se possiamo utilizzare i metodi a noi noti);
· UO: X=0.
5. Trova la derivata prima della funzione e i punti critici di prima specie.
6. Trova gli intervalli di monotonicità e gli estremi della funzione.
7. Trova la derivata seconda della funzione e i punti critici di secondo tipo.
8. Trova gli intervalli di convessità-concavità del grafico della funzione e i punti di flesso.
9. Trova gli asintoti del grafico della funzione.
10. Rappresentare graficamente la funzione. Quando costruisci, considera casi di possibile localizzazione del grafico in prossimità degli asintoti :
11. Se necessario, seleziona i punti di controllo per una costruzione più accurata.
Considera uno schema per studiare una funzione e tracciarne il grafico utilizzando esempi specifici:
Esempio 17.1. Traccia la funzione.
Soluzione. 1. Questa funzione definito sull'intera linea numerica ad eccezione di X=3, perché a questo punto il denominatore va a zero.
2. Per determinare l'uguaglianza e la disparità della funzione, troviamo:
Lo vediamo e, quindi, la funzione non è né pari né dispari.
3. La funzione non è periodica.
4. Trova i punti di intersezione con gli assi delle coordinate. Per trovare il punto di intersezione con l'asse OH accettare A=0. Otteniamo l'equazione: . Quindi, il punto (0; 0) è il punto di intersezione con gli assi delle coordinate.
5. Trova la derivata della funzione secondo la regola di derivazione di una frazione: = = = = .
Per trovare i punti critici, troviamo i punti in cui la derivata della funzione è uguale a 0 o non esiste.
Se =0, quindi, . Il prodotto è quindi 0 quando almeno uno dei fattori è 0: oppure .
X-3) 2 è uguale a 0, cioè non esiste a X=3.
La funzione presenta quindi tre punti critici del primo tipo: ; ; .
6. Sull'asse reale segniamo i punti critici del primo tipo, e segniamo il punto con un punto forato, perché non definisce una funzione.
Disporre i segni della derivata = su ciascun intervallo:
|
|
Negli intervalli dove , la funzione originale aumenta (a (-∞;0] ), dove - diminuisce (a ).
Punto X=0 è il punto massimo della funzione. Per trovare il massimo della funzione, troviamo il valore della funzione nel punto 0: .
Punto X=6 è il punto minimo della funzione. Per trovare il minimo della funzione, troviamo il valore della funzione al punto 6: .
I risultati della ricerca possono essere inseriti nella tabella. Il numero di righe nella tabella è fisso e pari a quattro, mentre il numero di colonne dipende dalla funzione studiata. Nelle celle della prima riga vengono inseriti in sequenza gli intervalli in cui i punti critici dividono il dominio della definizione di funzione, compresi i punti critici stessi. Per evitare errori nella costruzione dei punti che non appartengono all'area di definizione, è possibile non includerli nella tabella.
La seconda riga della tabella contiene i segni della derivata su ciascuno degli intervalli considerati e il valore della derivata nei punti critici. Secondo i segni della derivata della funzione, nella terza riga sono segnati gli intervalli di aumento, diminuzione ed estremi della funzione.
L'ultima riga viene utilizzata per indicare il massimo e il minimo della funzione.
| X | (-∞;0) | (0;3) | (3;6) | (6;+ ∞) | |||
| + | - | - | + | ||||
| f(x) | |||||||
| conclusioni | massimo | min |
7. Trova la derivata seconda della funzione come derivata della derivata prima: = =
Estrarre al numeratore X-3 fuori dalle parentesi e fai la riduzione:
Presentiamo al numeratore termini simili: .
Troviamo i punti critici del secondo tipo: punti in cui la derivata seconda della funzione è uguale a zero o non esiste.
0 se =0. Questa frazione non può essere uguale a zero, quindi non ci sono punti in cui la derivata seconda della funzione è uguale a zero.
Non esiste se il denominatore ( X-3) 3 è 0, cioè non esiste a X=3. :OH , UO, origine, unità di misura per ciascun asse.
Prima di tracciare una funzione, è necessario:
disegna asintoti con linee tratteggiate;
segnare i punti di intersezione con gli assi coordinati;
|
· Utilizzando i dati ottenuti sugli intervalli di aumento, diminuzione, convessità e concavità, costruire un grafico della funzione. I rami del grafico dovrebbero "tendere" agli asintoti, ma non attraversarli.
Controllare se il grafico della funzione corrisponde allo studio: se la funzione è pari o dispari, allora se viene rispettata la simmetria; se gli intervalli teoricamente trovati di aumento e diminuzione, convessità e concavità, punti di flesso.
11. Per una costruzione più precisa, puoi selezionare più punti di controllo. Ad esempio, troviamo i valori della funzione ai punti -2 e 7:
Regoliamo il grafico tenendo conto dei punti di controllo.
Domande di controllo:
- Qual è l'algoritmo per tracciare un grafico di funzione?
- Può una funzione avere un estremo in punti che non appartengono al dominio di definizione?
CAPITOLO 3. 3. CALCOLO INTEGRALE DELLA FUNZIONE
Asintoti del grafico di una funzione
Il fantasma dell'asintoto vaga per il sito da molto tempo per materializzarsi finalmente in un unico articolo e portare particolare gioia ai lettori perplessi studio completo delle funzioni. Trovare gli asintoti del grafico è una delle poche parti dell'attività specificata che viene trattata corso scolastico solo in una visione d'insieme, poiché attorno al calcolo ruotano gli eventi limiti di funzione, ma appartengono ancora alla matematica superiore. Visitatori poco esperti di analisi matematica, penso che il suggerimento sia comprensibile ;-) ... stop-stop, dove stai andando? limiti- è facile!
Esempi di asintoti incontrati immediatamente nella prima lezione su grafici di funzioni elementari, e ora l'argomento sta ricevendo una considerazione approfondita.
Allora cos'è un asintoto?
Immaginare punto variabile, che "viaggia" lungo il grafico della funzione. L'asintoto è Dritto, a cui chiusura illimitata il grafico della funzione si avvicina man mano che il suo punto variabile va all'infinito.
Nota : la definizione è significativa, se occorre una formulazione nella notazione dell'analisi matematica si rimanda al libro di testo.
Su un piano gli asintoti si classificano in base alla loro disposizione naturale:
1) Asintoti verticali, che sono dati da un'equazione della forma , dove "alfa" - numero reale. Il rappresentante popolare definisce lo stesso asse y,
con un attacco di lieve nausea, ricordiamo l'iperbole.
2) Asintoti obliqui scritto tradizionalmente equazione della linea retta con un fattore di pendenza. A volte un caso speciale viene individuato come un gruppo separato - asintoti orizzontali. Ad esempio, la stessa iperbole con asintoto .
Andiamo subito, entriamo in argomento con una breve raffica automatica:
Quanti asintoti può avere il grafico di una funzione?
Nessuno, uno, due, tre... o un numero infinito. Non andremo lontano per gli esempi, ricorderemo funzioni elementari. Parabola, parabola cubica e sinusoide non hanno alcun asintoto. grafico esponenziale, funzione logaritmica ha un asintoto unico. L'arcotangente, l'arcotangente ne ha due, e la tangente, la cotangente ne ha un numero infinito. Non è raro che un grafico abbia sia asintoti orizzontali che verticali. Iperbole, ti amerò sempre.
Cosa significa ?
Asintoti verticali di un grafico di una funzione
L'asintoto verticale di un grafico è solitamente nel punto dell'infinito funzioni. È semplice: se in un punto la funzione subisce una rottura infinita, allora la retta data dall'equazione è l'asintoto verticale del grafico.
Nota : nota che la notazione è usata per denotare due perfetti concetti diversi. Il punto è implicito o l'equazione di una linea retta - dipende dal contesto.
Quindi, per stabilire la presenza di un asintoto verticale in un punto, è sufficiente dimostrarlo almeno una da limiti unilaterali 
infinito. Molto spesso questo è il punto in cui si trova il denominatore della funzione zero. In effetti, abbiamo già trovato gli asintoti verticali negli ultimi esempi della lezione. sulla continuità della funzione. Ma in alcuni casi esiste solo un limite unilaterale, e se è infinito, allora di nuovo: ama e favorisci l'asintoto verticale. L'illustrazione più semplice: e l'asse y (vedi. Grafici e proprietà delle funzioni elementari).
Da quanto sopra segue anche il fatto ovvio: se la funzione è continua, allora non ci sono asintoti verticali. Per qualche motivo mi è venuta in mente una parabola. In effetti, dove puoi "attaccare" una linea retta qui? ... sì... capisco... i seguaci di zio Freud si accalcavano in preda all'isterismo =)
In genere non è vera l'affermazione contraria: ad esempio, la funzione non è definita su tutta la retta reale, ma è completamente priva di asintoti.
Asintoti obliqui di un grafico di una funzione
Gli asintoti obliqui (come caso speciale - orizzontale) possono essere tracciati se l'argomento della funzione tende a "più infinito" o "meno infinito". Ecco perché il grafico di una funzione non può avere più di due asintoti obliqui. Ad esempio, il grafico di una funzione esponenziale ha un singolo asintoto orizzontale in , e il grafico dell'arcotangente in ha due di questi asintoti, e diversi.
Quando il grafico qua e là si avvicina all'unico asintoto obliquo, è consuetudine unire gli “infiniti” sotto un'unica voce. Ad esempio, ... hai indovinato: .
Regola generale:
Se ce ne sono due finale limite 
, allora la retta è l'asintoto obliquo del grafico della funzione in . Se almeno una dei limiti sopra indicati è infinito, allora non esiste un asintoto obliquo.
Nota : le formule restano valide se "x" tende solo a "più infinito" o solo a "meno infinito".
Mostriamo che la parabola non ha asintoti obliqui: 
Il limite è infinito, quindi non esiste un asintoto obliquo. Si noti che nel trovare il limite 
non è più necessario perché la risposta è già stata ricevuta.
Nota
: se hai (o avrai) difficoltà a comprendere i segni più-meno, meno-più consulta l'aiuto all'inizio della lezione
sulle funzioni infinitesime, dove ho spiegato come interpretare correttamente questi segni.
È ovvio che anche qualsiasi funzione quadratica, cubica, polinomio di 4o grado e superiore non ha asintoti obliqui.
E ora assicuriamoci che anche il grafico non abbia un asintoto obliquo. Per scoprire l'incertezza, usiamo La regola dell'Hopital:
, che era da verificare.
Quando la funzione cresce indefinitamente, tuttavia, non esiste una linea retta a cui avvicinarsi il suo grafico infinitamente vicino.
Passiamo alla parte pratica della lezione:
Come trovare gli asintoti di un grafico di una funzione?
Ecco come viene formulato un compito tipico che consiste nel trovare TUTTI gli asintoti del grafico (verticale, obliquo/orizzontale). Anche se, per essere più precisi nella formulazione della domanda, stiamo parlando di uno studio sulla presenza di asintoti (dopotutto potrebbe non essercene affatto). Cominciamo con qualcosa di semplice:
Esempio 1
Trovare gli asintoti del grafico di una funzione
SoluzioneÈ conveniente suddividerlo in due punti:
1) Per prima cosa controlliamo se ci sono asintoti verticali. Il denominatore svanisce in , ed è subito chiaro che a questo punto la funzione soffre divario infinito, e la retta data dall'equazione è l'asintoto verticale del grafico della funzione . Ma prima di giungere a tale conclusione, è necessario trovare dei limiti unilaterali: 
Ti ricordo la tecnica di calcolo, su cui anch'io mi sono soffermato nell'articolo Continuità della funzione. punti di interruzione. Nell'espressione sotto il segno limite, al posto di "x" sostituiamo . Non c'è niente di interessante nel numeratore:
.
Ma nel denominatore risulta infinitesimale un numero negativo
:
, determina il destino del limite.
Il limite di sinistra è infinito e, in linea di principio, è già possibile emettere un verdetto sulla presenza di un asintoto verticale. Ma i limiti unilaterali non sono necessari solo per questo: AIUTANO A COMPRENDERE, COME individuare il grafico della funzione e tracciarlo CORRETTAMENTE. Dobbiamo quindi calcolare anche il limite destro: 
Conclusione: i limiti unilaterali sono infiniti, il che significa che la linea è un asintoto verticale del grafico della funzione in .
Primo limite finito, il che significa che è necessario “continuare la conversazione” e trovare il secondo limite:
Anche il secondo limite finito.
Quindi il nostro asintoto è:
Conclusione: la retta data dall'equazione è l'asintoto orizzontale del grafico della funzione in .
Trovare l'asintoto orizzontale
Puoi usare la formula semplificata:
Se esiste finito limite , allora la linea è l'asintoto orizzontale del grafico della funzione in .
È facile vedere che il numeratore e il denominatore della funzione un ordine di crescita, il che significa che il limite desiderato sarà finito: 
Risposta:
A seconda delle condizioni, non è necessario completare il disegno, ma se è in pieno svolgimento ricerca funzionale, quindi sulla bozza facciamo subito uno schizzo: 
Sulla base dei tre limiti trovati, prova a capire in modo indipendente come può essere posizionato il grafico della funzione. Abbastanza difficile? Trova 5-6-7-8 punti e segnali sul disegno. Tuttavia, il grafico di questa funzione è costruito utilizzando trasformazioni del grafico della funzione elementare, e i lettori che hanno esaminato attentamente l'Esempio 21 di questo articolo indovineranno facilmente di che tipo di curva si tratta.
Esempio 2
Trovare gli asintoti del grafico di una funzione
Questo è un esempio per soluzione indipendente. Il processo, ti ricordo, è convenientemente diviso in due punti: asintoti verticali e asintoti obliqui. Nella soluzione campione l'asintoto orizzontale viene trovato utilizzando uno schema semplificato.
In pratica, le funzioni frazionarie-razionali si incontrano più spesso e, dopo l'allenamento sulle iperboli, complicheremo il compito:
Esempio 3
Trovare gli asintoti del grafico di una funzione 
Soluzione: Uno, due e fatto:
1) Si trovano gli asintoti verticali nei punti di infinita discontinuità, quindi devi controllare se il denominatore va a zero. Decideremo equazione quadrata:
Il discriminante è positivo, quindi l'equazione ha due radici reali e il lavoro viene aggiunto in modo significativo =) 
Per trovare ulteriormente i limiti unilaterali è conveniente fattorizzare il trinomio quadrato:
(per la notazione compatta, il "meno" è stato introdotto nella prima parentesi). Per sicurezza eseguiremo un controllo, mentalmente o su tiraggio, aprendo le parentesi.
Riscriviamo la funzione nella forma 
Trovare i limiti unilaterali nel punto: 
E al punto: 
Pertanto, le rette sono gli asintoti verticali del grafico della funzione in esame.
2) Se guardi la funzione 
, allora è abbastanza ovvio che il limite sarà finito e avremo un asintoto orizzontale. Mostriamolo in breve: 
Pertanto, la linea retta (ascissa) è l'asintoto orizzontale del grafico di questa funzione.
Risposta:
I limiti e gli asintoti trovati forniscono molte informazioni sul grafico della funzione. Prova a immaginare mentalmente il disegno, tenendo conto dei seguenti fatti: 
Disegna la tua versione del grafico su una bozza.
Naturalmente i limiti riscontrati non determinano inequivocabilmente il tipo di grafico, e potreste commettere errori, ma l'esercizio stesso vi sarà di inestimabile aiuto durante studio completo delle funzioni. L'immagine corretta è alla fine della lezione.
Esempio 4
Trovare gli asintoti del grafico di una funzione
Esempio 5
Trovare gli asintoti del grafico di una funzione 
Questi sono compiti per una decisione indipendente. Entrambi i grafici hanno ancora una volta asintoti orizzontali, che vengono immediatamente rilevati dalle seguenti caratteristiche: nell'Esempio 4 ordine di crescita denominatore Di più rispetto all'ordine di crescita del numeratore e nell'esempio 5 il numeratore e il denominatore un ordine di crescita. Nella soluzione campione, la prima funzione viene indagata in modo completo per la presenza di asintoti obliqui e la seconda - attraverso il limite .
Gli asintoti orizzontali, secondo la mia impressione soggettiva, sono notevolmente più comuni di quelli "veramente inclinati". Caso generale tanto atteso:
Esempio 6
Trovare gli asintoti del grafico di una funzione 
Soluzione: classici del genere:
1) Poiché il denominatore è positivo, la funzione continuo sull'intera linea numerica e non ci sono asintoti verticali. …È buono? Non è la parola giusta: eccellente! L'articolo n. 1 è chiuso.
2) Verificare la presenza di asintoti obliqui:
Primo limite finito, quindi andiamo avanti. Durante il calcolo del secondo limite da eliminare incertezza "infinito meno infinito" portiamo l'espressione ad un denominatore comune: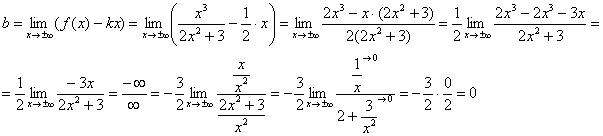 
Anche il secondo limite finito, quindi, il grafico della funzione in esame ha un asintoto obliquo:
Conclusione:
Quindi, per il grafico della funzione 
infinitamente vicino si avvicina ad una linea retta: 
Nota che interseca il suo asintoto obliquo all'origine, e tali punti di intersezione sono abbastanza accettabili: è importante che "tutto sia normale" all'infinito (in realtà, stiamo parlando di asintoti esattamente lì).
Esempio 7
Trovare gli asintoti del grafico di una funzione
Soluzione: non c'è molto da commentare, quindi redigerò un esempio approssimativo di soluzione finale:
1) Asintoti verticali. Esploriamo il punto.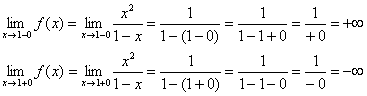 
La linea retta è l'asintoto verticale del grafico in .
2) Asintoti obliqui: 
La linea retta è l'asintoto obliquo del grafico in .
Risposta: 
I limiti unilaterali e gli asintoti trovati ci consentono di assumere con elevata certezza come appare il grafico di questa funzione. Disegno corretto alla fine della lezione.
Esempio 8
Trovare gli asintoti del grafico di una funzione
Questo è un esempio di soluzione indipendente, per comodità di calcolo di alcuni limiti è possibile dividere il numeratore per il denominatore termine per termine. E ancora, analizzando i risultati, prova a disegnare un grafico di questa funzione.
Ovviamente i proprietari degli asintoti obliqui "reali" sono i grafici di quelle funzioni frazionarie-razionali per le quali il grado più alto del numeratore uno in più il grado più alto del denominatore. Se di più, non ci sarà alcun asintoto obliquo (ad esempio, ).
Ma nella vita accadono altri miracoli:
Esempio 9
Esempio 11
Esaminare il grafico di una funzione per gli asintoti
Soluzione: è ovvio 
consideriamo quindi solo il semipiano destro, dove è presente il grafico della funzione.
Pertanto, la linea retta (asse y) è l'asintoto verticale per il grafico della funzione in .
2) Lo studio dell'asintoto obliquo può essere effettuato secondo lo schema completo, ma nell'articolo Regolamento dell'Hospital lo abbiamo scoperto funzione lineare ordine di crescita superiore a quello logaritmico, quindi: 
(vedi esempio 1 della stessa lezione).
Conclusione: l'asse delle ascisse è l'asintoto orizzontale del grafico della funzione in .
Risposta:
, Se ;
, Se .
Disegno per chiarezza: 
È interessante notare che una funzione apparentemente simile non ha alcun asintoto (chi lo desidera può verificarlo).
Due esempi finali di studio autonomo:
Esempio 12
Esaminare il grafico di una funzione per gli asintoti 
Se la distanza d dal punto della curva y \u003d f (x), che ha un ramo infinito, a una linea retta definita tende a zero mentre il punto si sposta lungo questa curva verso l'infinito, allora la linea retta è chiamata asintoto della curva.
Ci sono asintoti: 1) orizzontale, 2) verticale e 3) obliquo.
1. La curva y \u003d f (x) ha un asintoto orizzontale y \u003d b solo se esiste un limite finito della funzione f (x) in , e questo limite è uguale a b, cioè se
2. La curva y \u003d f (x) ha un asintoto verticale x \u003d a, se in . Per determinare gli asintoti verticali è necessario trovare quei valori dell'argomento in prossimità dei quali f(x) aumenta in valore assoluto senza limiti. Se tali valori dell'argomento sono a1, a2, ..., allora le equazioni degli asintoti verticali saranno
x \u003d a1, x \u003d a2 ...
3. Per determinare l'asintoto obliquo y \u003d kx + b della curva y \u003d f (x), è necessario trovare i numeri k e b dalle formule
(i casi dovrebbero essere considerati separatamente). Esistono asintoti obliqui per la curva y = f(x) se e solo se questi limiti sono finiti. Nel determinare questi limiti è conveniente utilizzare la regola di L'Hospital.
Esempio. Trova gli asintoti della curva 
Soluzione. Non esistono asintoti orizzontali. Troviamo l'asintoto verticale dalla condizione
2x + 3 = 0 => x = - 3/2, mentre y 
, Quando 
, sì 
, Quando 
. Definiamo asintoti obliqui, la cui equazione ha la forma: y = kx + b
Poiché k e b hanno valori finiti e sono uguali tra loro in x 
e a x 
, allora esiste un unico asintoto obliquo la cui equazione
Studio delle funzioni generali
Uno studio completo di una funzione è solitamente inteso come la soluzione di tali domande:
Determinare l'ambito di una funzione.
Rivelare la questione delle funzioni pari e dispari.
Definizione dei punti di interruzione delle funzioni.
Determinazione degli asintoti del grafico di una funzione.
Definizione degli intervalli di aumento e diminuzione della funzione.
Determinazione dell'estremo di una funzione.
Determinazione degli intervalli di convessità e concavità del grafico della funzione.
Definizione dei punti di flesso.
Trovare l'intersezione con gli assi delle coordinate.
Tracciare una funzione.
Esempio. Esplorando la funzione 
D(y)=( 
). La funzione è continua su tutto il dominio di definizione. Non ci sono punti di interruzione.
La funzione non è né pari, né dispari, né periodica.
Non ci sono punti di interruzione.
Non ci sono asintoti verticali; 
, non ci sono asintoti obliqui.
5,
6.
. Punti critici x = -2, x = 0.
|
( |
( |
||||
|
Cartello |
|
| |||
|
Comportamento della funzione |
Crescente |
3 |
Crescente |
)
)
=
0
7,
8.
,
in x = 1, 
non esiste per x = 0.
|
( |
( |
||||
|
Cartello |
|
| |||
|
Comportamento della funzione |
Parte superiore convessa |
Non un punto di flesso |
Parte superiore convessa |
punto di flesso |
convesso verso il basso |
)
)
=
=
09.
x=0 e x=-5.
Esercizio 1
Calcolare il determinante della matrice A del secondo ordine
Calcolare il determinante della matrice B del terzo ordine
Calcola il determinante della matrice B espandendolo in qualsiasi riga e colonna
Calcola il determinante della matrice B, utilizzando le proprietà dei determinanti. Ridurre il calcolo del determinante del terzo ordine al calcolo di un determinante del secondo ordine
|
opzione 1 | ||||||||||||||||||
|
opzione 2 | ||||||||||||||||||
|
Opzione 3 | ||||||||||||||||||
|
Opzione 4 | ||||||||||||||||||
|
Opzione 5 | ||||||||||||||||||
|
Opzione 6 | ||||||||||||||||||
|
Opzione 7 | ||||||||||||||||||
|
Opzione 8 | |||||||||||
|
Opzione 9 | |||||||||||
|
Opzione 10 | |||||||||||
Compito 2
1. Risolvi il sistema di equazioni utilizzando il metodo di Cramer Ah = a
Risolvere il sistema di equazioni con il metodo di Cramer INX = B
Risolvere il sistema di equazioni utilizzando il metodo di Gauss INX = B
Compito 3.
Ah = a
Risolvere il sistema di equazioni con il metodo matriciale INX = B
Compito 4.
Calcolare il rango di una matrice.
1.
,
2.
;
3.
4.
5.
6.
7.
8
9.
10.
Compito 5
Dati due vertici di un triangolo Δ ABC: A (X 1 , sì 1 ), IN(X 2 , sì 2 ) e punto D (X 3 , sì 3 ) intersezioni di altezze:
a) creare un'equazione di altezze, mediane, bisettrici di un triangolo Δ ABC.
b) trovare le equazioni delle rette passanti per i vertici del triangolo e parallele ai lati.
c) determinare le lunghezze delle altezze del triangolo e la distanza dal punto M (X 4 , sì 4 ) ai lati del triangolo.
|
X 1 |
sì 1 |
X 2 |
sì 2 |
X 3 |
sì 3 |
X 4 |
sì 4 |
|
Compito 6.
Date le coordinate dei vertici della piramide ABCD: UN (X 1 , sì 1 , z 1 ), IN(X 2 , sì 2 , z 3 ) ,C (X 2 , sì 2 , z 2 ) ,D (X 4 , sì 4 , z 3 )
1) lunghezza della costola AB;.
2) angolo tra le nervature AB E UND;
3) un angolo tra un bordo ANNO DOMINI e bordo ABC;
4) zona del viso ABC;
5) il volume della piramide;
6) Equazione di una retta AB;
7) equazione del piano ABC;
8) l'equazione dell'altezza abbassata dall'alto D fino all'orlo ABC.
|
N |
X 1 |
sì 1 |
z 1 |
X 2 |
sì 2 |
z 2 |
X 3 |
sì 3 |
z 3 |
X 4 |
sì 4 |
z 4 |
Compito 7.
Attività 8. Trova il dominio della funzione
5.
7.
8.
9.
10.
Attività 9. Rappresentare graficamente la funzione
1.
2.
3.
4
5.
6.
7.
8.
9.
10.
Compito 10. Trova i limiti della funzione
1.a) 
, B) 
, V) 
,
G) 
, e) 
2.a) 
, B) 
, V) 
,
G) 
, e) 
3.a) 
, B) 
, V) 
,
G) 
, e) 
4.a) 
, B) 
, V) 
,
G) 
, e) 
5.a) 
, B) 
, V) 
,
G) 
, e) 
6.a) 
, B) 
, V) 
,
G) 
, e) 
7.a) 
, B) 
, V) 
,
G) 
, e) 
8.a) 
, B) 
, V) 
,
G) 
, e) 
9.a) 
, B) 
, V) 
,
G) 
, e) 
10.a) 
, B) 
, V) 
,
G) 
, e) 
Compito 11. Trova la derivata
1.
, B),
V) 
, G) 
, e) 
, e) 
2.a) 
, B) 
, V) 
,
G) 
, e) 
,e) 
3.a), b) 
, V) 
, G) 
, e) 
, e) 
4.a) 
, B) 
, V) 
,
G) 
, e) 
, e) 
5.a) 
, B) 
, V) 
, G) 
, e) 
,
e) 
6.a) 
, B) 
, V) 
, G) 
, e) 
,
e) 
7.a) 
, B),
V) 
, G) 
, e) 
,
e) 
8.a) 
, B) 
, V) 
, G) 
, e) 
,
e) 
9.a) 
, B) 
, V) 
,
G) 
, e) 
, e) 
10.a) 
, B) 
, V) 
,
G) 
, e) 
, e) 
Attività 12. Mostra che la funzione soddisfa l'uguaglianza
Compito 13. Trova la derivata seconda di una funzione data parametricamente.
1 .
6.
2.
7
3.
8
4.
9.
5.
10.
Compito 14. Trova i limiti utilizzando la regola di L'Hospital
Compito 15. Trova gli estremi delle funzioni date.
1.
6.
2.
7.
3.
8.
4.
9.
5.
10.
Attività 16. Trova il valore più grande e più piccolo sui segmenti specificati e agli intervalli specificati.
Compito 17. Conduci uno studio completo di queste funzioni e disegna i loro grafici.
1.
6.
2.
7.
3.
8.
4.
9.
5.
10.
Letteratura:
Bavrin I.I. Corso di matematica superiore.-M.: Illuminismo, 1992.-400 p.
Bronstein I.N., Semendyaev K.A. Manuale di matematica. M, 1967, 608 s
Corso generale di matematica superiore per economisti, a cura di V.I. Ermakov-M. "Infra-M".1999 - 655 pag.
Teush V.L. Corso di matematica superiore. - M .: Scienza sovietica, 1958, 270 p.
Shipachev V.S. Matematica superiore: Esercitazione M. Scuola superiore, 1990.-479s.
Matematica superiore per economisti: libro di testo per le scuole superiori / N.Sh. Kremer, B.A. Putko e altri; M: UNITI, 2002. - 461 p.
Val'ev K.G., Dzhalladova I.A. Aiutante.
La soluzione può essere opportunamente suddivisa in due parti:
1) Per prima cosa controlliamo se ci sono asintoti verticali. Il denominatore si annulla, ed è subito chiaro che a questo punto la funzione subisce una discontinuità infinita, e la retta data dall'equazione è l'asintoto verticale del grafico della funzione. Ma prima di giungere a tale conclusione, è necessario trovare dei limiti unilaterali:
Ti ricordo la tecnica di calcolo, di cui ho parlato analogamente nell'articolo Continuità di una funzione. Punti di interruzione. Nell'espressione sotto il segno del limite, invece di "x" sostituiamo. Non c'è niente di interessante nel numeratore:
Ma al denominatore si ottiene un numero negativo infinitamente piccolo:
Determina il destino del limite.
Il limite di sinistra è infinito e, in linea di principio, è già possibile emettere un verdetto sulla presenza di un asintoto verticale. Ma i limiti unilaterali sono necessari non solo per questo: TI AIUTANO A CAPIRE COME si trova il grafico della funzione e a costruirlo CORRETTAMENTE. Dobbiamo quindi calcolare anche il limite destro:
Conclusione: i limiti unilaterali sono infiniti, il che significa che la retta è un asintoto verticale del grafico della funzione a.
Il primo limite è finito, il che significa che è necessario “continuare la conversazione” e trovare il secondo limite:
Anche il secondo limite è finito.
Quindi il nostro asintoto è:
Conclusione: la retta data dall'equazione è l'asintoto orizzontale del grafico della funzione a.
Per trovare l'asintoto orizzontale, puoi utilizzare una formula semplificata:
Se esiste un limite finito, la linea è un asintoto orizzontale del grafico della funzione a.
È facile vedere che numeratore e denominatore della funzione sono dello stesso ordine di crescita, il che significa che il limite desiderato sarà finito:
A seconda delle condizioni, non è necessario completare il disegno, ma se lo studio della funzione è in pieno svolgimento, eseguiamo immediatamente uno schizzo sulla bozza:
Sulla base dei tre limiti trovati, prova a capire in modo indipendente come può essere posizionato il grafico della funzione. Abbastanza difficile? Trova 5-6-7-8 punti e segnali sul disegno. Tuttavia, il grafico di questa funzione è costruito utilizzando le trasformazioni del grafico di una funzione elementare, e i lettori che hanno esaminato attentamente l'Esempio 21 di questo articolo indovineranno facilmente di che tipo di curva si tratta.
Questo è un esempio fai da te. Il processo, ti ricordo, è convenientemente diviso in due punti: asintoti verticali e asintoti obliqui. Nella soluzione campione l'asintoto orizzontale viene trovato utilizzando uno schema semplificato.
In pratica, le funzioni frazionarie-razionali si incontrano più spesso e, dopo l'allenamento sulle iperboli, complicheremo il compito:
Trovare gli asintoti del grafico di una funzione
Soluzione: Uno, due e fatto:
1) Gli asintoti verticali si trovano in punti di discontinuità infinita, quindi bisogna verificare se il denominatore si annulla. Decideremo equazione quadrata:
Il discriminante è positivo, quindi l'equazione ha due radici reali e c'è molto lavoro da aggiungere
Per trovare ulteriormente i limiti unilaterali, è conveniente fattorizzare il trinomio quadrato:
(per la notazione compatta, il "meno" è stato introdotto nella prima parentesi). Per sicurezza eseguiremo un controllo, mentalmente o su tiraggio, aprendo le parentesi.
Riscriviamo la funzione nella forma
Trova i limiti unilaterali in un punto:
Limite della funzione del grafico asintotico
E al punto:
Pertanto, le rette sono gli asintoti verticali del grafico della funzione in esame.
2) Se guardi la funzione, è abbastanza ovvio che il limite sarà finito e abbiamo un asintoto orizzontale. Mostriamolo in breve:
Pertanto, la linea retta (ascissa) è l'asintoto orizzontale del grafico di questa funzione.
I limiti e gli asintoti trovati forniscono molte informazioni sul grafico della funzione. Prova a immaginare mentalmente il disegno, tenendo conto dei seguenti fatti:
Disegna la tua versione del grafico su una bozza.
Naturalmente, i limiti rilevati non determinano in modo inequivocabile il tipo di grafico e potresti commettere un errore, ma l'esercizio stesso sarà di inestimabile aiuto nel corso di uno studio completo della funzione. L'immagine corretta è alla fine della lezione.
Trovare gli asintoti del grafico di una funzione
Trovare gli asintoti del grafico di una funzione
Questi sono compiti per una decisione indipendente. Entrambi i grafici hanno ancora una volta asintoti orizzontali, che vengono immediatamente rilevati dalle seguenti caratteristiche: nell'Esempio 4, il denominatore aumenta in un ordine di grandezza maggiore del numeratore, e nell'Esempio 5, il numeratore e il denominatore sono dello stesso ordine di crescita. Nella soluzione campione, la prima funzione viene indagata in modo completo per la presenza di asintoti obliqui e la seconda - attraverso il limite.
Gli asintoti orizzontali, secondo la mia impressione soggettiva, sono notevolmente più comuni di quelli "veramente inclinati". Caso generale tanto atteso:
Trovare gli asintoti del grafico di una funzione
Soluzione: classica del genere:
- 1) Poiché il denominatore è positivo, la funzione è continua su tutta la linea numerica e non ci sono asintoti verticali. …È buono? Non è la parola giusta: fantastico! L'articolo n. 1 è chiuso.
- 2) Verificare la presenza di asintoti obliqui:
Anche il secondo limite è finito, quindi il grafico della funzione in esame ha un asintoto obliquo:
Pertanto, in , il grafico della funzione è infinitamente vicino a una linea retta.
Si noti che interseca il suo asintoto obliquo all'origine, e tali punti di intersezione sono abbastanza accettabili: è importante che "tutto sia normale" all'infinito (in realtà, è lì che emerge la discussione sugli asintoti).
Trovare gli asintoti del grafico di una funzione
Soluzione: non c'è molto da commentare, quindi redigerò un esempio approssimativo di soluzione finale:
1) Asintoti verticali. Esploriamo il punto.
La linea retta è l'asintoto verticale del grafico a.
2) Asintoti obliqui:
La retta è l'asintoto obliquo della trama a.
I limiti unilaterali e gli asintoti trovati ci consentono di assumere con elevata certezza come appare il grafico di questa funzione.
Trovare gli asintoti del grafico di una funzione
Questo è un esempio di soluzione indipendente, per comodità di calcolo di alcuni limiti è possibile dividere il numeratore per il denominatore termine per termine. E ancora, analizzando i risultati, prova a disegnare un grafico di questa funzione.
Ovviamente, i proprietari degli asintoti obliqui "reali" sono i grafici di quelle funzioni frazionarie-razionali il cui grado più alto del numeratore è maggiore di uno maggiore del grado più alto del denominatore. Se di più, non ci sarà alcun asintoto obliquo (ad esempio).
Ma nella vita accadono anche altri miracoli.