Հորիզոնական ասիմպտոտը որոշելու քայլեր. Ինչպե՞ս գտնել ֆունկցիայի գրաֆիկի ասիմպտոտները: Քանի՞ ասիմպտոտ կարող է ունենալ ֆունկցիայի գրաֆիկը:

Ֆունկցիայի գրաֆիկի ասիմպտոտ y \u003d f (x) կոչվում է այն գիծ, ​​որն ունի այն հատկությունը, որ հեռավորությունը (x, f (x)) կետից մինչև այս ուղիղը ձգտում է զրոյի՝ գրաֆիկի կետի սկզբնակետից անսահմանափակ հեռացնելով:

Նկար 3.10. տրված են գրաֆիկական օրինակներ ուղղահայաց, հորիզոնականԵվ թեքասիմպտոտ.

Գրաֆիկի ասիմպտոտները գտնելը հիմնված է հետևյալ երեք թեորեմների վրա.

Ուղղահայաց ասիմպտոտի թեորեմ. Թող y \u003d f (x) ֆունկցիան սահմանվի x 0 կետի ինչ-որ հարևանությամբ (հնարավոր է՝ բացառելով հենց այս կետը), և ֆունկցիայի միակողմանի սահմաններից առնվազն մեկը հավասար լինի անսահմանությանը, այսինքն. Այնուհետև x \u003d x 0 տողը y \u003d f (x) ֆունկցիայի գրաֆիկի ուղղահայաց ասիմպտոտն է:

Ակնհայտ է, որ x \u003d x 0 տողը չի կարող լինել ուղղահայաց ասիմպտոտ, եթե ֆունկցիան շարունակական է x 0 կետում, քանի որ այս դեպքում . Հետևաբար, ուղղահայաց ասիմպտոտները պետք է փնտրել ֆունկցիայի անջատման կետերում կամ դրա տիրույթի ծայրերում:

Թեորեմ հորիզոնական ասիմպտոտի վրա. Թող y \u003d f (x) ֆունկցիան սահմանվի բավականաչափ մեծ x-ի համար և լինի ֆունկցիայի վերջավոր սահման: Այնուհետև y = b ուղիղը ֆունկցիայի գրաֆիկի հորիզոնական ասիմպտոտն է։

Մեկնաբանություն. Եթե ​​սահմաններից միայն մեկն է վերջավոր, ապա ֆունկցիան ունի համապատասխանաբար. ձախակողմյանկամ աջակողմյանհորիզոնական ասիմպտոտ:

Այն դեպքում, երբ ֆունկցիան կարող է ունենալ թեք ասիմպտոտ:

Շեղ ասիմպտոտի թեորեմ. Թող y = f(x) ֆունկցիան սահմանվի բավականաչափ մեծ x-ի համար և լինեն վերջավոր սահմաններ . Այնուհետև y = kx + b ուղիղը ֆունկցիայի գրաֆիկի թեք ասիմպտոտն է։

Առանց ապացույցի.

Թեք ասիմպտոտը, ինչպես նաև հորիզոնականը, կարող է լինել աջակողմյան կամ ձախակողմյան, եթե համապատասխան սահմանների հիմքը որոշակի նշանի անսահմանությունն է։

Ֆունկցիաների ուսումնասիրությունը և դրանց գրաֆիկների կառուցումը սովորաբար ներառում է հետևյալ քայլերը.

1. Գտեք ֆունկցիայի տիրույթը:

2. Հետազոտիր զույգ-կենտ ֆունկցիան:

3. Գտե՛ք ուղղահայաց ասիմպտոտները՝ ուսումնասիրելով սահմանման տիրույթի սահմանների վրա անջատման կետերը և ֆունկցիայի վարքը, եթե դրանք վերջավոր են։

4. Գտե՛ք հորիզոնական կամ թեք ասիմպտոտներ՝ ուսումնասիրելով ֆունկցիայի վարքը անվերջության ժամանակ:

5. Գտի՛ր ֆունկցիայի միապաղաղության ծայրահեղությունները և միջակայքերը:

6. Գտե՛ք ֆունկցիայի ուռուցիկության միջակայքերը և թեքման կետերը:

7. Գտեք կոորդինատների առանցքների հետ հատման կետերը և, հնարավոր է, որոշ լրացուցիչ կետեր, որոնք ճշգրտում են գրաֆիկը:

Ֆունկցիայի դիֆերենցիալ

Կարելի է ապացուցել, որ եթե ֆունկցիան ունի որոշ բազայի սահմանաչափ, որը հավասար է վերջնական համարը, ապա այն կարող է ներկայացվել որպես այս թվի գումար և նույն հիմքով անվերջ փոքր արժեք (և հակառակը).

Այս թեորեմը կիրառենք դիֆերենցիալ ֆունկցիայի նկատմամբ.

Այսպիսով, Dy ֆունկցիայի աճը բաղկացած է երկու անդամից՝ 1) գծային Dx-ի նկատմամբ, այսինքն. f`(x)Dx; 2) ոչ գծային Dx-ի նկատմամբ, այսինքն. a(Dx)Dx. Միևնույն ժամանակ, քանի որ , այս երկրորդ անդամը ավելի բարձր կարգի անվերջ փոքր է, քան Dx-ը (քանի որ Dx-ը ձգտում է զրոյի, այն նույնիսկ ավելի արագ է հակված զրոյի):

Դիֆերենցիալֆունկցիան կոչվում է ֆունկցիայի աճի հիմնական, գծային՝ Dx մասի նկատմամբ, արտադրանքին հավասարանկախ փոփոխականի աճող ածանցյալ dy = f `(x)Dх.

Գտե՛ք y = x ֆունկցիայի դիֆերենցիալը:

Քանի որ dy = f `(x)Dx = x`Dx = Dx, ապա dx = Dx, այսինքն. անկախ փոփոխականի դիֆերենցիալը հավասար է այդ փոփոխականի աճին:

Հետևաբար, ֆունկցիայի դիֆերենցիալի բանաձևը կարելի է գրել dy = f `(x)dх: Այդ իսկ պատճառով ածանցյալի նշաններից մեկը dy/dх կոտորակն է։

Դիֆերենցիալի երկրաչափական նշանակությունը պատկերված է
նկար 3.11. Վերցրեք կամայական M(x, y) կետը y = f(x) ֆունկցիայի գրաֆիկի վրա: Եկեք x արգումենտին տանք հավելում Dx: Այնուհետև y = f(x) ֆունկցիան կստանա ավելացում Dy = f(x + Dх) - f(x): Գծենք M կետի ֆունկցիայի գրաֆիկին շոշափող, որը x-ի առանցքի դրական ուղղության հետ կազմում է a անկյուն, այսինքն. f `(x) = tg a. Սկսած ուղղանկյուն եռանկյուն MKN
KN \u003d MN * tg a \u003d Dx * tg a \u003d f `(x) Dx \u003d dy.

Այսպիսով, ֆունկցիայի դիֆերենցիալը տվյալ կետում ֆունկցիայի գրաֆիկին գծված շոշափողի օրդինատի աճն է, երբ x-ը մեծանում է Dx-ով:

Դիֆերենցիալի հատկությունները հիմնականում նույնն են, ինչ ածանցյալի հատկությունները.

3. d(u ± v) = du ± dv.

4. d(uv) = v du + u dv.

5. d(u/v) = (v du - u dv)/v 2:

Այնուամենայնիվ, կա ֆունկցիայի դիֆերենցիալի մի կարևոր հատկություն, որը չունի նրա ածանցյալը. սա է դիֆերենցիալ ձևի անփոփոխություն.

y = f(x) ֆունկցիայի դիֆերենցիալի սահմանումից դիֆերենցիալը dy = f`(x)dх է: Եթե ​​այս y ֆունկցիան բարդ է, այսինքն. y = f(u), որտեղ u = j(x), ապա y = f և f `(x) = f `(u)*u`: Ապա dy = f`(u)*u`dx: Բայց ֆունկցիայի համար
u = j(x) դիֆերենցիալ du = u`dx: Այստեղից dy = f `(u)*du:

Համեմատելով dy = f `(x)dх և dy = f `(u)*du հավասարությունները, մենք համոզվում ենք, որ դիֆերենցիալ բանաձևը չի փոխվում, եթե x անկախ փոփոխականի ֆունկցիայի փոխարեն մենք դիտարկենք մի ֆունկցիա. կախյալ փոփոխական u. Դիֆերենցիալի այս հատկությունը կոչվում է դիֆերենցիալի ձևի (կամ բանաձևի) անփոփոխություն (այսինքն՝ անփոփոխություն):

Այնուամենայնիվ, այս երկու բանաձևերում դեռ կա տարբերություն. դրանցից առաջինում անկախ փոփոխականի դիֆերենցիալը հավասար է այս փոփոխականի աճին, այսինքն. dx = Dx, իսկ երկրորդում du ֆունկցիայի դիֆերենցիալը միայն այս Du ֆունկցիայի աճի գծային մասն է, և միայն փոքր Dх du » Du-ի համար։

1. Ասիմպտոտների հայեցակարգը

Մեկը հանգրվաններգծագրման ֆունկցիաները ասիմպտոտներ գտնելն է: Մենք մեկ անգամ չէ, որ հանդիպել ենք ասիմպտոտների հետ. ֆունկցիաները գծագրելիս, y=tgx, y=ctgx. Մենք դրանք սահմանել ենք որպես գծեր, որոնց «հակված» է ֆունկցիայի գրաֆիկը, բայց երբեք չի հատվում: Ժամանակն է տալ ասիմպտոտների ճշգրիտ սահմանումը:

Ասիմպտոտների երեք տեսակ կա՝ ուղղահայաց, հորիզոնական և թեք։ Գծագրում ասիմպտոտները սովորաբար նշվում են կետագծերով։

Դիտարկենք հետևյալ արհեստականորեն գծագրված ֆունկցիայի գրաֆիկը (նկ. 16.1), որի օրինակով հստակ տեսանելի են բոլոր տեսակի ասիմպտոտները.

Ասիմպտոտի յուրաքանչյուր տեսակի համար մենք տալիս ենք սահմանում.

1. Ուղղակի x=aկանչեց ուղղահայաց ասիմպտոտ գործառույթները, եթե.

2. Ուղղակի y=sկանչեց հորիզոնական ասիմպտոտ գործառույթները, եթե.

3. Ուղղակի y=kx+bկանչեց թեք ասիմպտոտ գործառույթները, եթե.

Երկրաչափորեն, թեք ասիմպտոտի սահմանումը նշանակում է, որ երբ →∞ ֆունկցիայի գրաֆիկը մոտենում է ուղիղ գծին կամայականորեն փակված y=kx+b, այսինքն. դրանք գործնականում նույնն են: Տարբերությունը գործնականում է միանման արտահայտություններձգտում է զրոյի:

Նշենք, որ հորիզոնական և թեք ասիմպտոտները դիտարկվում են միայն →∞ պայմանով: Երբեմն դրանք տարբերվում են հորիզոնական և թեք ասիմպտոտների՝ →+∞ և →-∞:

1. Ասիմպտոտի որոնման ալգորիթմ

Ասիմպտոտներ գտնելու համար կարող է օգտագործվել հետևյալ ալգորիթմը.

Կարող է լինել մեկ ուղղահայաց ասիմպտոտ, մի քանի կամ ընդհանրապես չկա:

• Եթե ​​c-ն թիվ է, ապա y=sհորիզոնական ասիմպտոտն է;
• Եթե ​​c-ն անվերջություն է, ապա հորիզոնական ասիմպտոտներ չկան:

Եթե ​​ֆունկցիան երկու բազմանդամների հարաբերություն է, ապա եթե ֆունկցիան ունի հորիզոնական ասիմպտոտներ, մենք չենք փնտրի թեք ասիմպտոտներ՝ դրանք գոյություն չունեն:

Դիտարկենք ֆունկցիայի ասիմպտոտները գտնելու օրինակներ.

Օրինակ 16.1.Գտե՛ք կորի ասիմպտոտները:

Լուծում X-1≠0; X≠1.

Եկեք ստուգենք, արդյոք գիծը կա x= 1 ուղղահայաց ասիմպտոտ: Դա անելու համար մենք հաշվարկում ենք ֆունկցիայի սահմանը կետում x= 1: .

x= 1 - ուղղահայաց ասիմպտոտ:

Հետ= .

Հետ= = . Որովհետեւ Հետ=2 (թիվ), ապա y=2հորիզոնական ասիմպտոտն է։

Քանի որ ֆունկցիան բազմանդամների հարաբերակցություն է, հորիզոնական ասիմպտոտների առկայության դեպքում մենք պնդում ենք, որ թեք ասիմպտոտներ չկան:

x= 1-ը և հորիզոնական ասիմպտոտը y=2.Պարզության համար այս ֆունկցիայի գրաֆիկը ներկայացված է Նկ. 16.2.

Օրինակ 16.2. Գտե՛ք կորի ասիմպտոտները:

Լուծում. 1. Գտեք ֆունկցիայի տիրույթը՝ X-2≠0; X≠2.

Եկեք ստուգենք, արդյոք գիծը կա x= 2 ուղղահայաց ասիմպտոտ: Դա անելու համար մենք հաշվարկում ենք ֆունկցիայի սահմանը կետում x= 2: .

Մենք ստացանք, հետևաբար, x= 2 - ուղղահայաց ասիմպտոտ:

2. Հորիզոնական ասիմպտոտներ որոնելու համար մենք գտնում ենք. Հետ= .

Քանի որ սահմանի մեջ կա անորոշություն, մենք օգտագործում ենք L'Hopital կանոնը. Հետ= = . Որովհետեւ Հետանսահմանություն է, ուրեմն հորիզոնական ասիմպտոտներ չկան։

3. Թեք ասիմպտոտներ որոնելու համար մենք գտնում ենք.

Մենք ստացել ենք ձևի անորոշություն, մենք օգտագործում ենք L'Hopital կանոնը՝ = =1: բըստ բանաձևի. .

b= = =

Դա հասկացա b= 2. Հետո y=kx+b –թեք ասիմպտոտ. Մեր դեպքում դա կարծես. y=x+2.

Բրինձ. 16.3

Այսպիսով, այս ֆունկցիան ունի ուղղահայաց ասիմպտոտ x= 2 և թեք ասիմպտոտ y=x+2.Պարզության համար ֆունկցիայի գրաֆիկը ներկայացված է Նկ. 16.3.

Վերահսկիչ հարցեր.

Դասախոսություն 17

Այս դասախոսության ընթացքում մենք կամփոփենք նախկինում ուսումնասիրված ողջ նյութը: Մեր երկար ճանապարհորդության վերջնական նպատակն այն է, որ կարողանանք ուսումնասիրել վերլուծականորեն տրված ցանկացած գործառույթ և կառուցել դրա գրաֆիկը: Մեր ուսումնասիրության կարևոր մասերը կլինեն ծայրահեղությունների ֆունկցիայի ուսումնասիրությունը, գրաֆիկի միապաղաղության, ուռուցիկության և գոգավորության միջակայքերի որոշումը, թեքման կետերի որոնումը, ֆունկցիայի գրաֆիկի ասիմպտոտները:

Հաշվի առնելով վերը նշված բոլոր ասպեկտները՝ ներկայացնում ենք ֆունկցիան ուսումնասիրելու և գծագրելու սխեմա .

1. Գտեք ֆունկցիայի տիրույթը:

2. Հետազոտեք զույգ-կենտի ֆունկցիան.

եթե , ապա ֆունկցիան զույգ է (զույգ ֆունկցիայի գրաֆիկը սիմետրիկ է առանցքի նկատմամբ. OU);

եթե , ապա ֆունկցիան կենտ է (կենտ ֆունկցիայի գրաֆիկը սիմետրիկ է ծագման նկատմամբ);

Հակառակ դեպքում ֆունկցիան ոչ զույգ է, ոչ էլ կենտ։

3. Հետազոտել ֆունկցիան պարբերականության համար (մեր ուսումնասիրած ֆունկցիաներից միայն եռանկյունաչափական ֆունկցիաները կարող են պարբերական լինել):

4. Գտե՛ք ֆունկցիայի գրաֆիկի հատման կետերը կոորդինատային առանցքներով.

· Օ՜: ժամը=0 (մենք լուծում ենք հավասարումը միայն այն դեպքում, եթե կարողանանք օգտագործել մեզ հայտնի մեթոդները);

· OU: X=0.

5. Գտե՛ք ֆունկցիայի առաջին ածանցյալը և առաջին տեսակի կրիտիկական կետերը:

6. Գտե՛ք միապաղաղության միջակայքերը և ֆունկցիայի ծայրահեղությունները:

7. Գտե՛ք ֆունկցիայի երկրորդ ածանցյալը և երկրորդ տեսակի կրիտիկական կետերը:

8. Գտի՛ր ֆունկցիայի գրաֆիկի ուռուցիկություն-գոգավորության միջակայքերը և թեքման կետերը:

9. Գտե՛ք ֆունկցիայի գրաֆիկի ասիմպտոտները:

10. Գծապատկերե՛ք ֆունկցիան: Կառուցելիս հաշվի առեք ասիմպտոտների մոտ գծապատկերի հնարավոր գտնվելու դեպքերը :

11. Անհրաժեշտության դեպքում ընտրեք կառավարման կետեր ավելի ճշգրիտ շինարարության համար:

Դիտարկենք ֆունկցիան ուսումնասիրելու և դրա գրաֆիկը գծելու սխեման՝ օգտագործելով հատուկ օրինակներ.

Օրինակ 17.1. Գրեք ֆունկցիան:

Լուծում. 1. Այս գործառույթըսահմանված է ամբողջ թվային տողում, բացառությամբ X=3, քանի որ այս պահին հայտարարը գնում է զրոյի:

2. Ֆունկցիայի հավասարությունն ու տարօրինակությունը որոշելու համար գտնում ենք.

Մենք տեսնում ենք, որ և, հետևաբար, ֆունկցիան ոչ զույգ է, ոչ էլ կենտ:

3. Ֆունկցիան ոչ պարբերական է։

4. Գտի՛ր կոորդինատային առանցքների հետ հատման կետերը: Գտնել առանցքի հետ հատման կետը Օ՜ընդունել ժամը=0. Մենք ստանում ենք հավասարումը. Այսպիսով, կետը (0; 0) կոորդինատային առանցքների հետ հատման կետն է:

5. Գտե՛ք ֆունկցիայի ածանցյալը ըստ կոտորակի տարբերակման կանոնի՝ = = = = .

Կրիտիկական կետերը գտնելու համար մենք գտնում ենք այն կետերը, որոնցում ֆունկցիայի ածանցյալը հավասար է 0-ի կամ գոյություն չունի։

Եթե ​​=0, հետևաբար, . Այդ դեպքում արտադրյալը 0 է, երբ գործակիցներից առնվազն մեկը 0 է՝ կամ .

X-3) 2-ը հավասար է 0-ի, այսինքն. գոյություն չունի X=3.

Այսպիսով, ֆունկցիան ունի առաջին տեսակի երեք կրիտիկական կետեր. ; .

6. Իրական առանցքի վրա նշում ենք առաջին տեսակի կրիտիկական կետերը, իսկ կետը նշում ենք ծակված կետով, քանի որ. այն գործառույթ չի սահմանում:

Յուրաքանչյուր միջակայքի վրա դասավորե՛ք ածանցյալի նշանները.

տ.ր

t.max

Այն ընդմիջումներով, որտեղ , սկզբնական ֆունկցիան մեծանում է (-ում (-∞;0] ), որտեղ - նվազում է (at ):

Կետ X=0-ը ֆունկցիայի առավելագույն կետն է: Ֆունկցիայի առավելագույնը գտնելու համար 0 կետում գտնենք ֆունկցիայի արժեքը:

Կետ X=6-ը ֆունկցիայի նվազագույն կետն է: Ֆունկցիայի նվազագույնը գտնելու համար 6-րդ կետում գտնենք ֆունկցիայի արժեքը՝ .

Հետազոտության արդյունքները կարելի է մուտքագրել աղյուսակում։ Աղյուսակում տողերի թիվը ֆիքսված է և հավասար է չորսի, իսկ սյունակների քանակը կախված է ուսումնասիրվող ֆունկցիայից։ Առաջին շարքի բջիջներում հաջորդաբար մուտքագրվում են այն միջակայքերը, որոնցում կրիտիկական կետերը բաժանում են ֆունկցիայի սահմանման տիրույթը, ներառյալ հենց կրիտիկական կետերը: Սահմանման տարածքին չպատկանող կետեր կառուցելիս սխալներից խուսափելու համար կարելի է դրանք չներառել աղյուսակում:

Աղյուսակի երկրորդ շարքը պարունակում է ածանցյալի նշանները դիտարկված յուրաքանչյուր միջակայքում և ածանցյալի արժեքը կրիտիկական կետերում: Ֆունկցիայի ածանցյալի նշաններին համապատասխան երրորդ տողում նշվում են ֆունկցիայի ավելացման, նվազման և ծայրահեղությունների միջակայքերը։

Վերջին տողը օգտագործվում է ֆունկցիայի առավելագույնը և նվազագույնը նշելու համար։

X	(-∞;0)		(0;3)		(3;6)		(6;+ ∞)
	+		-		-		+
f(x)
եզրակացություններ		առավելագույնը				ր

7. Գտե՛ք ֆունկցիայի երկրորդ ածանցյալը՝ որպես առաջին ածանցյալի ածանցյալ՝ = =

Հանեք համարիչի մեջ X-3 փակագծերից դուրս և կատարեք կրճատումը.

Համարիչում ներկայացնում ենք նման տերմիններ.

Գտնենք երկրորդ տեսակի կրիտիկական կետեր. կետեր, որոնցում ֆունկցիայի երկրորդ ածանցյալը հավասար է զրոյի կամ գոյություն չունի:

0, եթե =0. Այս կոտորակը չի կարող հավասար լինել զրոյի, հետևաբար, չկան կետեր, որտեղ ֆունկցիայի երկրորդ ածանցյալը հավասար է զրոյի։

Գոյություն չունի, եթե հայտարարը ( X-3) 3-ը 0 է, այսինքն. գոյություն չունի X=3. :Օ, OU, ծագում, չափման միավորներ յուրաքանչյուր առանցքի համար։

Նախքան ֆունկցիա գծագրելը, դուք պետք է.

նկարել ասիմպտոտներ կետավոր գծերով;

նշեք հատման կետերը կոորդինատային առանցքներով.

Բրինձ. 17.1

նշեք ֆունկցիայի առավելագույնը և նվազագույնը, և խորհուրդ է տրվում ֆունկցիայի առավելագույնն ու նվազագույնը նշանակել անմիջապես գծագրի վրա կամարներով՝ k կամ ;

· Օգտագործելով ստացված տվյալները մեծացման, նվազման, ուռուցիկության և գոգավորության միջակայքերի վերաբերյալ՝ կառուցե՛ք ֆունկցիայի գրաֆիկը։ Գրաֆիկի ճյուղերը պետք է «հակեն» ասիմպտոտներին, բայց չհատեն դրանք:

Ստուգեք՝ արդյոք ֆունկցիայի գրաֆիկը համապատասխանում է ուսումնասիրությանը. եթե ֆունկցիան զույգ է, թե կենտ, ապա նկատվում է արդյոք համաչափությունը. արդյոք տեսականորեն հայտնաբերված աճի և նվազման, ուռուցիկության և գոգավորության միջակայքերը, թեքության կետերը:

11. Ավելի ճշգրիտ կառուցման համար կարող եք ընտրել մի քանի հսկիչ կետեր: Օրինակ, եկեք գտնենք ֆունկցիայի արժեքները -2 և 7 կետերում.

Գրաֆիկը կարգավորում ենք՝ հաշվի առնելով կառավարման կետերը։

Վերահսկիչ հարցեր.

1. Ո՞րն է ֆունկցիայի գրաֆիկը գծելու ալգորիթմը:
2. Կարո՞ղ է ֆունկցիան ծայրահեղություն ունենալ այն կետերում, որոնք չեն պատկանում սահմանման տիրույթին:

ԳԼՈՒԽ 3. 3. ՖՈՒՆԿՑԻԱՅԻ ԻՆՏԵԳՐԱԼ ՀԱՇՎԱՐԿ

Ֆունկցիայի գրաֆիկի ասիմպտոտներ

Ասիմպտոտի ուրվականը երկար ժամանակ թափառում էր կայքում, որպեսզի վերջապես նյութականանա մեկ հոդվածում և առանձնահատուկ ուրախություն պատճառի տարակուսած ընթերցողներին։ գործառույթի ամբողջական ուսումնասիրություն. Գրաֆիկի ասիմպտոտները գտնելը նշված առաջադրանքի մի քանի մասերից մեկն է, որը ծածկված է. դպրոցական դասընթացմիայն ակնարկով, քանի որ իրադարձությունները պտտվում են հաշվարկի շուրջ գործառույթի սահմանները, բայց նրանք դեռ պատկանում են բարձրագույն մաթեմատիկային։ Այցելուներ, ովքեր վատ տիրապետում են մաթեմատիկական վերլուծությանը, կարծում եմ ակնարկը հասկանալի է ;-) ... ստոպ-ստոպ, ո՞ւր ես գնում: սահմանները- հեշտ է!

Ասիմպտոտների օրինակները անմիջապես հանդիպեցին առաջին դասին տարրական ֆունկցիաների գրաֆիկներ, և այժմ թեման մանրամասն քննարկվում է։

Այսպիսով, ինչ է ասիմպտոտը:

Պատկերացնել փոփոխական կետ, որը «ճանապարհորդում» է ֆունկցիայի գրաֆիկով։ Ասիմպտոտն է ուղիղ, ինչին անսահմանափակ փակումֆունկցիայի գրաֆիկը մոտենում է, քանի որ նրա փոփոխական կետը գնում է դեպի անսահմանություն:

Նշում Սահմանումը իմաստալից է, եթե մաթեմատիկական վերլուծության նշման մեջ ձևակերպման կարիք ունեք, խնդրում ենք դիմել դասագրքին:

Հարթության վրա ասիմպտոտները դասակարգվում են ըստ իրենց բնական դասավորության.

1) Ուղղահայաց ասիմպտոտներ, որոնք տրված են ձևի հավասարմամբ, որտեղ «ալֆա» - իրական թիվ. Հանրաճանաչ ներկայացուցիչը ինքն է սահմանում y առանցքը,
մեղմ սրտխառնոցի նոպաով մենք հիշում ենք հիպերբոլիա:

2) Շեղ ասիմպտոտներավանդաբար գրված ուղիղ գծի հավասարումթեքության գործակիցով։ Երբեմն որպես առանձին խումբ առանձնացվում է հատուկ դեպք. հորիզոնական ասիմպտոտներ. Օրինակ, նույն հիպերբոլան ասիմպտոտով:

Շուտով մենք գնում ենք, եկեք թեմային հարվածենք կարճ ավտոմատ պոռթկումով.

Քանի՞ ասիմպտոտ կարող է ունենալ ֆունկցիայի գրաֆիկը:

Ոչ մեկը, մեկ, երկու, երեք... կամ անսահման թիվ: Օրինակների համար հեռու չենք գնա, կհիշենք տարրական գործառույթներ. Պարաբոլան, խորանարդ պարաբոլան, սինուսոիդն ընդհանրապես ասիմպտոտ չունեն: Էքսպոնենցիալ, լոգարիթմական ֆունկցիայի գրաֆիկն ունի մեկ ասիմպտոտ: Արկտանգենսը, արկոտանգենսն ունի դրանցից երկուսը, իսկ շոշափողը՝ կոտանգենսը՝ անսահման թիվ։ Հազվադեպ չէ, երբ գրաֆիկը ունի ինչպես հորիզոնական, այնպես էլ ուղղահայաց ասիմպտոտներ: Հիպերբոլ, միշտ կսիրի քեզ:

Ինչ է նշանակում ?

Ֆունկցիայի գրաֆիկի ուղղահայաց ասիմպտոտներ

Գրաֆիկի ուղղահայաց ասիմպտոտը սովորաբար անսահմանության կետումգործառույթները։ Դա պարզ է. եթե մի կետում ֆունկցիան անսահման ընդմիջում է ապրում, ապա հավասարման միջոցով տրված ուղիղ գիծը գրաֆիկի ուղղահայաց ասիմպտոտն է:

Նշում Նկատի ունեցեք, որ նշումն օգտագործվում է երկու կատարյալ նշանակելու համար տարբեր հասկացություններ. Կետը ենթադրվում է կամ ուղիղ գծի հավասարումը - կախված է համատեքստից:

Այսպիսով, որոշակի կետում ուղղահայաց ասիմպտոտի առկայությունը հաստատելու համար բավական է ցույց տալ դա գոնե մեկըմիակողմանի սահմաններից անվերջ. Ամենից հաճախ սա այն կետն է, որտեղ ֆունկցիայի հայտարարը զրո. Փաստորեն, դասի վերջին օրինակներում մենք արդեն գտել ենք ուղղահայաց ասիմպտոտներ: ֆունկցիայի շարունակականության վրա. Բայց որոշ դեպքերում կա միայն մեկ միակողմանի սահման, և եթե այն անսահման է, ապա նորից՝ սիրեք և կողմնորոշվեք ուղղահայաց ասիմպտոտին: Ամենապարզ նկարազարդումը և y առանցքը (տես. Տարրական ֆունկցիաների գրաֆիկները և հատկությունները).

Վերոնշյալից հետևում է նաև ակնհայտ փաստը. եթե ֆունկցիան միացված է շարունակական, ապա ուղղահայաց ասիմպտոտներ չկան. Չգիտես ինչու, մտքում պարաբոլա եկավ։ Իսկապես, որտեղ կարելի է այստեղ ուղիղ գիծ «կպցնել»: ... այո ... հասկանում եմ ... քեռի Ֆրեյդի հետևորդները կուչ են եկել հիստերիկայի մեջ =)

Ընդհակառակը, ընդհանուր առմամբ, ճիշտ չէ. օրինակ, ֆունկցիան սահմանված չէ ամբողջ իրական գծի վրա, բայց այն ամբողջովին զրկված է ասիմպտոտներից:

Ֆունկցիայի գրաֆիկի թեք ասիմպտոտներ

Շեղ (որպես հատուկ դեպք՝ հորիզոնական) ասիմպտոտները կարող են գծվել, եթե ֆունկցիայի արգումենտը հակված է դեպի «գումարած անսահմանություն» կամ «մինուս անսահմանություն»։ Ահա թե ինչու ֆունկցիայի գրաֆիկը չի կարող ունենալ ավելի քան երկու թեք ասիմպտոտ. Օրինակ, էքսպոնենցիալ ֆունկցիայի գրաֆիկն ունի մեկ հորիզոնական ասիմպտոտ ժամը , իսկ աղեղի շոշափողի գրաֆիկը ունի երկու այդպիսի ասիմպտոտ և տարբեր:

Երբ այս ու այն կողմ գրաֆիկը մոտենում է միակ թեք ասիմպտոտին, ապա ընդունված է միավորել «անվերջությունները» մեկ մուտքի տակ։ Օրինակ, ... ճիշտ եք գուշակել.

Ընդհանուր կանոն:

Եթե ​​կան երկու եզրափակիչսահման , ապա ուղիղ գիծը ֆունկցիայի գրաֆիկի թեք ասիմպտոտն է ժամը . Եթե գոնե մեկըվերը նշված սահմաններից անսահման է, ապա թեք ասիմպտոտ չկա:

Նշում Բանաձևերը մնում են վավեր, եթե «x»-ը հակված է միայն «գումարած անսահմանությանը» կամ միայն «մինուս անսահմանությանը»:

Եկեք ցույց տանք, որ պարաբոլան չունի թեք ասիմպտոտներ.

Սահմանը անսահման է, ուստի թեք ասիմպտոտ չկա: Նկատի ունեցեք, որ սահմանը գտնելիս այլևս կարիք չկա, քանի որ պատասխանն արդեն ստացվել է։

Նշում Եթե ​​դուք դժվարանում եք (կամ կունենաք) հասկանալու գումարած-մինուս, մինուս-պլյուս նշանները, խնդրում ենք տեսնել օգնությունը դասի սկզբում:
անվերջ փոքր ֆունկցիաների մասին, որտեղ ես ասացի, թե ինչպես ճիշտ մեկնաբանել այս նշանները:

Ակնհայտ է, որ 4-րդ և ավելի բարձր աստիճանի ցանկացած քառակուսի, խորանարդ ֆունկցիա, բազմանդամը նույնպես չունի թեք ասիմպտոտներ։

Եվ հիմա եկեք համոզվենք, որ գրաֆիկը նույնպես չունի թեք ասիմպտոտ: Անորոշությունը բացահայտելու համար մենք օգտագործում ենք L'Hopital-ի կանոն:
, որը պետք է ստուգվեր։

Այնուամենայնիվ, երբ ֆունկցիան անորոշ ժամանակով աճում է, չկա այնպիսի ուղիղ գիծ, ​​որին կմոտենա դրա գրաֆիկը անսահման մոտ.

Անցնենք դասի գործնական մասին.

Ինչպե՞ս գտնել ֆունկցիայի գրաֆիկի ասիմպտոտները:

Այսպես է ձևակերպվում տիպիկ առաջադրանքը, որը ներառում է գրաֆիկի ԲՈԼՈՐ ասիմպտոտների (ուղղահայաց, թեք/հորիզոնական) հայտնաբերում: Թեև, ավելի ճիշտ հարցի ձևակերպման մեջ, խոսքը ասիմպտոտների առկայության ուսումնասիրության մասին է (ի վերջո, կարող է ընդհանրապես չլինել)։ Սկսենք մի պարզ բանից.

Օրինակ 1

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

ԼուծումՀարմար է այն բաժանել երկու կետի.

1) Նախ ստուգում ենք՝ արդյոք կան ուղղահայաց ասիմպտոտներ։ Հայտարարը անհետանում է , և անմիջապես պարզ է դառնում, որ այս պահին ֆունկցիան տուժում է անվերջ բացը, իսկ հավասարմամբ տրված ուղիղը ֆունկցիայի գրաֆիկի ուղղահայաց ասիմպտոտն է։ Բայց նման եզրակացություն անելուց առաջ անհրաժեշտ է գտնել միակողմանի սահմաններ.

Հիշեցնում եմ ձեզ հաշվարկման տեխնիկան, որի վրա ես նույնպես անդրադարձել եմ հոդվածում Գործառույթների շարունակականություն: ընդմիջման կետեր. Սահմանային նշանի տակ արտահայտության մեջ «x»-ի փոխարեն փոխարինում ենք . Համարիչում հետաքրքիր բան չկա.
.

Բայց հայտարարում ստացվում է անսահման փոքր բացասական թիվ :
, այն որոշում է սահմանի ճակատագիրը։

Ձախ կողմի սահմանը անսահման է, և, սկզբունքորեն, արդեն հնարավոր է դատավճիռ կայացնել ուղղահայաց ասիմպտոտի առկայության վերաբերյալ: Բայց միակողմանի սահմաններ են պետք ոչ միայն դրա համար, դրանք ՕԳՆՈՒՄ ԵՆ ՀԱՍԿԱՆԵԼ, ԻՆՉՊԵՍգտնվում է ֆունկցիայի գրաֆիկը և գծագրել այն ՃԻՇՏ. Հետևաբար, մենք պետք է նաև հաշվարկենք աջակողմյան սահմանը.

Եզրակացությունմիակողմանի սահմանները անսահման են, ինչը նշանակում է, որ տողը հանդիսանում է ֆունկցիայի գրաֆիկի ուղղահայաց ասիմպտոտը:

Առաջին սահմանը վերջավոր, ինչը նշանակում է, որ անհրաժեշտ է «շարունակել զրույցը» և գտնել երկրորդ սահմանը.

Երկրորդ սահմանը նույնպես վերջավոր.

Այսպիսով, մեր ասիմպտոտը հետևյալն է.

ԵզրակացությունՀավասարմամբ տրված ուղիղ գիծը ֆունկցիայի գրաֆիկի հորիզոնական ասիմպտոտն է.

Հորիզոնական ասիմպտոտը գտնելու համար
Դուք կարող եք օգտագործել պարզեցված բանաձևը:

Եթե ​​գոյություն ունի վերջավորսահմանը, ապա տողը ֆունկցիայի գրաֆիկի հորիզոնական ասիմպտոտն է ժամը .

Հեշտ է տեսնել, որ ֆունկցիայի համարիչն ու հայտարարը աճի մեկ կարգ, ինչը նշանակում է, որ ցանկալի սահմանը վերջնական կլինի.

Պատասխանել:

Ըստ պայմանի` ոչ թե պետք է ավարտին հասցնել գծագիրը, այլ եթե ամբողջ թափով ֆունկցիոնալ հետազոտություն, այնուհետև նախագծի վրա մենք անմիջապես կազմում ենք էսքիզ.

Գտնված երեք սահմանների հիման վրա փորձեք ինքնուրույն պարզել, թե ինչպես կարող է տեղակայվել ֆունկցիայի գրաֆիկը: Բավական դժվար? Գտե՛ք 5-6-7-8 կետերը և նշե՛ք գծագրության վրա։ Այնուամենայնիվ, այս ֆունկցիայի գրաֆիկը կառուցված է օգտագործելով տարրական ֆունկցիայի գրաֆիկի փոխակերպումները, և ընթերցողները, ովքեր ուշադիր ուսումնասիրել են այս հոդվածի 21-րդ օրինակը, հեշտությամբ կկռահեն, թե դա ինչ կորի է:

Օրինակ 2

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

Սա օրինակ է անկախ որոշում. Գործընթացը, հիշեցնում եմ ձեզ, հարմար կերպով բաժանվում է երկու կետի՝ ուղղահայաց ասիմպտոտների և թեք ասիմպտոտների: Նմուշի լուծույթում հորիզոնական ասիմպտոտը հայտնաբերվում է պարզեցված սխեմայի միջոցով:

Գործնականում ամենից հաճախ հանդիպում են կոտորակային-ռացիոնալ ֆունկցիաներ, և հիպերբոլաների վրա մարզվելուց հետո մենք կբարդացնենք խնդիրը.

Օրինակ 3

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

ԼուծումՄեկ, երկու և արված.

1) հայտնաբերված են ուղղահայաց ասիմպտոտները անսահման ընդհատման կետերում, այնպես որ դուք պետք է ստուգեք, արդյոք հայտարարը գնում է զրոյի: Մենք կորոշենք քառակուսի հավասարում:

Տարբերիչը դրական է, ուստի հավասարումն ունի երկու իրական արմատ, և աշխատանքը զգալիորեն ավելացվում է =)

Միակողմանի սահմանները հետագայում գտնելու համար հարմար է քառակուսի եռանկյունը ֆակտորիզացնել:
(կոմպակտ նշման համար «մինուսը» ներկայացվել է առաջին փակագծում): Անվտանգության ցանցի համար մենք ստուգում կկատարենք մտովի կամ ցամաքի վրա՝ բացելով փակագծերը։

Եկեք վերագրենք ֆունկցիան ձևով

Գտեք միակողմանի սահմաններ այս կետում.

Եվ կետում.

Այսպիսով, ուղիղ գծերը դիտարկվող ֆունկցիայի գրաֆիկի ուղղահայաց ասիմպտոտներն են։

2) Եթե նայեք գործառույթին , ապա միանգամայն ակնհայտ է, որ սահմանը վերջնական է լինելու, և մենք ունենք հորիզոնական ասիմպտոտ։ Եկեք դա ցույց տանք կարճ ձևով.

Այսպիսով, ուղիղ գիծը (abscissa) այս ֆունկցիայի գրաֆիկի հորիզոնական ասիմպտոտն է։

Պատասխանել:

Գտնված սահմանները և ասիմպտոտները շատ տեղեկություններ են տալիս ֆունկցիայի գրաֆիկի մասին։ Փորձեք մտովի պատկերացնել գծանկարը՝ հաշվի առնելով հետևյալ փաստերը.

Սևագրի վրա ուրվագծեք գրաֆիկի ձեր տարբերակը:

Իհարկե, հայտնաբերված սահմանները միանշանակ չեն որոշում գրաֆիկի տեսակը, և դուք կարող եք սխալվել, բայց վարժությունն ինքնին անգնահատելի օգնություն կլինի ընթացքում: գործառույթի ամբողջական ուսումնասիրություն. Ճիշտ նկարը դասի վերջում է:

Օրինակ 4

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

Օրինակ 5

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

Սրանք անկախ որոշման առաջադրանքներ են։ Երկու գրաֆիկներն էլ ունեն հորիզոնական ասիմպտոտներ, որոնք անմիջապես հայտնաբերվում են հետևյալ հատկանիշներով. Օրինակ 4-ում աճի կարգըհայտարար ավելինքան համարիչի աճի կարգը, իսկ օրինակ 5-ում համարիչը և հայտարարը աճի մեկ կարգ. Նմուշի լուծույթում առաջին ֆունկցիան ամբողջությամբ ուսումնասիրվում է թեք ասիմպտոտների առկայության համար, իսկ երկրորդը՝ սահմանի միջով:

Հորիզոնական ասիմպտոտները, իմ սուբյեկտիվ տպավորությամբ, նկատելիորեն ավելի տարածված են, քան «իսկապես թեքվածները»: Երկար սպասված ընդհանուր դեպք.

Օրինակ 6

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

Լուծումժանրի դասականներ.

1) Քանի որ հայտարարը դրական է, ֆունկցիան շարունակականամբողջ թվային տողի վրա, և ուղղահայաց ասիմպտոտներ չկան: …Լավ է? Ճիշտ բառ չէ՝ հիանալի: Թիվ 1 կետը փակ է:

2) Ստուգեք թեք ասիմպտոտների առկայությունը.

Առաջին սահմանը վերջավոր, ուրեմն անցնենք առաջ։ Ընթացքում հաշվարկման երկրորդ սահմանաչափի վերացնել անորոշություն «անսահմանություն մինուս անսահմանություն»արտահայտությունը բերում ենք ընդհանուր հայտարարի.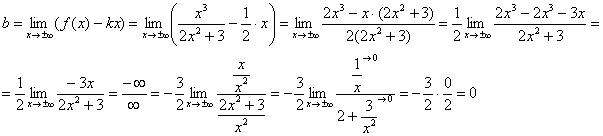

Երկրորդ սահմանը նույնպես վերջավորՀետևաբար, դիտարկվող ֆունկցիայի գրաֆիկն ունի թեք ասիմպտոտ.

Եզրակացություն:

Այսպիսով, ֆունկցիայի գրաֆիկի համար անսահման մոտմոտենում է ուղիղ գծին.

Նկատի ունեցեք, որ այն սկզբում հատում է իր թեք ասիմպտոտը, և նման հատման կետերը միանգամայն ընդունելի են. կարևոր է, որ «ամեն ինչ նորմալ է» անսահմանության մեջ (իրականում խոսքը հենց այնտեղ ասիմպտոտների մասին է):

Օրինակ 7

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

ԼուծումՄեկնաբանելու շատ բան չկա, ուստի վերջնական լուծման մոտավոր նմուշ կկազմեմ.

1) Ուղղահայաց ասիմպտոտներ. Եկեք ուսումնասիրենք կետը: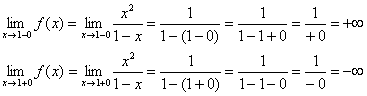

Ուղիղ գիծը սյուժեի ուղղահայաց ասիմպտոտն է ժամը .

2) թեք ասիմպտոտներ.

Ուղիղ գիծը գծապատկերի թեք ասիմպտոտն է:

Պատասխանել:

Գտնված միակողմանի սահմանները և ասիմպտոտները մեզ թույլ են տալիս բարձր հստակությամբ ենթադրել, թե ինչպիսին է այս ֆունկցիայի գրաֆիկը: Դասի վերջում ճիշտ նկարել:

Օրինակ 8

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

Սա անկախ լուծման օրինակ է, որոշ սահմաններ հաշվարկելու հարմարության համար կարող եք համարիչը բաժանել հայտարարի անդամով: Եվ կրկին, վերլուծելով արդյունքները, փորձեք նկարել այս ֆունկցիայի գրաֆիկը։

Ակնհայտ է, որ «իրական» թեք ասիմպտոտների տերերը այն կոտորակային-ռացիոնալ ֆունկցիաների գրաֆիկներն են, որոնց համար համարիչի ամենաբարձր աստիճանը. եւս մեկհայտարարի ամենաբարձր աստիճանը. Եթե ​​ավելի շատ լինի, ապա չի լինի թեք ասիմպտոտ (օրինակ՝ ):

Բայց կյանքում տեղի են ունենում այլ հրաշքներ.

Օրինակ 9

Օրինակ 11

Ուսումնասիրեք ֆունկցիայի գրաֆիկը ասիմպտոտների համար

Լուծում:Դա ակնհայտ է , հետևաբար, մենք դիտարկում ենք միայն աջ կիսահարթությունը, որտեղ կա ֆունկցիայի գրաֆիկ։

Այսպիսով, ուղիղ գիծը (y առանցքը) ֆունկցիայի գրաֆիկի ուղղահայաց ասիմպտոտն է .

2) թեք ասիմպտոտի ուսումնասիրությունը կարող է իրականացվել ամբողջական սխեմայի համաձայն, սակայն հոդվածում. L'Hospital-ի կանոններըմենք դա պարզեցինք գծային ֆունկցիաաճի ավելի բարձր կարգ, քան լոգարիթմական, հետևաբար. (տե՛ս նույն դասի օրինակ 1):

Եզրակացություն. աբսցիսային առանցքը ֆունկցիայի գրաֆիկի հորիզոնական ասիմպտոտն է .

Պատասխանել:
, Եթե ;
, Եթե .

Նկարչություն պարզության համար.

Հետաքրքիր է, որ թվացյալ նման ֆունկցիան ընդհանրապես ասիմպտոտ չունի (ցանկանողները կարող են ստուգել սա):

Ինքնուսումնասիրության երկու վերջնական օրինակ.

Օրինակ 12

Ուսումնասիրեք ֆունկցիայի գրաֆիկը ասիմպտոտների համար

Եթե ​​d հեռավորությունը կորի y \u003d f (x) կետից, որն ունի անվերջ ճյուղ, մինչև որոշ որոշակի ուղիղ գիծը ձգտում է զրոյի, երբ կետը շարժվում է այս կորի երկայնքով դեպի անսահմանություն, ապա ուղիղ գիծը կոչվում է ասիմպտոտ: կորի.

Կան ասիմպտոտներ՝ 1) հորիզոնական, 2) ուղղահայաց և 3) թեք։

1. y \u003d f (x) կորը ունի հորիզոնական ասիմպտոտ y \u003d b միայն այն դեպքում, եթե կա f (x) ֆունկցիայի վերջավոր սահմանը ժամը , և այս սահմանը հավասար է b-ի, այսինքն՝ եթե

2. y \u003d f (x) կորը ունի ուղղահայաց ասիմպտոտ x \u003d a, եթե ժամը . Ուղղահայաց ասիմպտոտները որոշելու համար անհրաժեշտ է գտնել փաստարկի այն արժեքները, որոնց մոտ f(x) բացարձակ արժեքով մեծանում է առանց սահմանի: Եթե ​​փաստարկի նման արժեքներն են a1, a2, ..., ապա ուղղահայաց ասիմպտոտների հավասարումները կլինեն.

x \u003d a1, x \u003d a2 ...

3. y \u003d kx + b կորի y \u003d f (x) թեք ասիմպտոտը որոշելու համար բանաձևերից պետք է գտնել k և b թվերը:

(դեպքերը պետք է դիտարկել առանձին): y = f(x) կորի թեք ասիմպտոտներ գոյություն ունեն, եթե և միայն այն դեպքում, երբ այդ սահմանները վերջավոր են: Այս սահմանները որոշելիս հարմար է օգտագործել L'Hospital-ի կանոնը։

Օրինակ. Գտեք կորի ասիմպտոտներ

Լուծում. Հորիզոնական ասիմպտոտներ չկան։ Մենք պայմանից գտնում ենք ուղղահայաց ասիմպտոտը

2x + 3 = 0 => x = - 3/2, մինչդեռ y
, Երբ
, յ
, Երբ
. Սահմանում ենք թեք ասիմպտոտներ, որոնց հավասարումն ունի ձև՝ y = kx + b.

Քանի որ k-ն և b-ն ունեն վերջավոր արժեքներ և x-ում հավասար են միմյանց
և x-ում
, ապա կա եզակի թեք ասիմպտոտ, որի հավասարումը

Ընդհանուր գործառույթների ուսումնասիրություն

Ֆունկցիայի ամբողջական ուսումնասիրությունը սովորաբար հասկացվում է որպես այսպիսի հարցերի լուծում.

Գործառույթի շրջանակի որոշում.

Զույգ և կենտ ֆունկցիաների հարցի բացահայտում:

Ֆունկցիայի ընդմիջման կետերի սահմանում:

Ֆունկցիայի գրաֆիկի ասիմպտոտների որոշում.

Ֆունկցիայի ավելացման և նվազման միջակայքերի սահմանում:

Ֆունկցիայի ծայրահեղության որոշում:

Ֆունկցիայի գրաֆիկի ուռուցիկության և գոգավորության միջակայքերի որոշում.

Շեղման կետերի սահմանում.

Գտնելով հատումը կոորդինատային առանցքների հետ:

Ֆունկցիայի գրաֆիկի գծագրում:

Օրինակ. Գործառույթի ուսումնասիրություն

D(y)=(
) Ֆունկցիան շարունակական է սահմանման ողջ տիրույթում: Ընդմիջման կետեր չկան:

Ֆունկցիան ոչ զույգ է, ոչ կենտ կամ պարբերական:

Ընդմիջման կետեր չկան:

Ուղղահայաց ասիմպտոտներ չկան.
, թեք ասիմպտոտներ չկան։

5, 6.
. Կրիտիկական կետեր x = -2, x = 0:

	( )				( )
Նշան		= 0
Գործառույթի վարքագիծ	Աճող	3			Աճող

7, 8.
,
x = 1,
գոյություն չունի x = 0-ի համար:

	( )				( )
Նշան		=		= 0
Գործառույթի վարքագիծ	Ուռուցիկ վերև	Շեղման կետ չէ	Ուռուցիկ վերև	թեքման կետ	ուռուցիկ ներքեւ

9.
x=0 և x=-5:

Վարժություն 1

Հաշվե՛ք երկրորդ կարգի Ա մատրիցի որոշիչը

Հաշվե՛ք երրորդ կարգի B մատրիցի որոշիչը

Հաշվե՛ք B մատրիցի որոշիչը՝ ընդլայնելով այն ցանկացած տողում և սյունակում

Հաշվե՛ք B մատրիցի որոշիչը՝ օգտագործելով որոշիչների հատկությունները: Կրճատել երրորդ կարգի որոշիչի հաշվարկը մեկ երկրորդ կարգի որոշիչի հաշվարկի վրա

Տարբերակ 1

Տարբերակ 2

Տարբերակ 3

Տարբերակ 4

Տարբերակ 5

Տարբերակ 6

Տարբերակ 7

Տարբերակ 8
Տարբերակ 9
Տարբերակ 10

Առաջադրանք 2

1.Հավասարումների համակարգը լուծիր Քրամերի մեթոդով Ահ = ա

Հավասարումների համակարգը լուծիր Քրամերի մեթոդով INx = բ

Լուծե՛ք հավասարումների համակարգը Գաուսի մեթոդով INx = բ

Առաջադրանք 3.

Ահ = ա

Լուծե՛ք հավասարումների համակարգը մատրիցային մեթոդով INx = բ

Առաջադրանք 4.

Հաշվեք մատրիցայի աստիճանը:

1., 2.
;

3.
4.

5.
6.

7.
8

9.
10.

Առաջադրանք 5

Տրվում է Δ եռանկյան երկու գագաթ ABC: Ա (X 1 , յ 1 ), IN(X 2 , յ 2 ) և կետ Դ (x 3 , y 3 ) բարձրությունների խաչմերուկներ.

ա) Կազմե՛ք Δ եռանկյան բարձրությունների, միջինների, կիսորդների հավասարում ABC.

բ) գտե՛ք եռանկյան գագաթներով անցնող և կողմերին զուգահեռ ուղիղների հավասարումները.

գ) որոշել եռանկյան բարձրությունների երկարությունները և կետից հեռավորությունը Մ (X 4 , յ 4 ) դեպի եռանկյան կողմերը:

	x 1	y 1	x 2	y 2	x 3	y 3	x 4	y 4

Առաջադրանք 6.

Տրվում են բուրգի գագաթների կոորդինատները ABCԴ: Ա (X 1 , յ 1 , զ 1 ), IN(X 2 , յ 2 , զ 3 ) ,Գ (x 2 , y 2 , զ 2 ) ,Դ (X 4 , յ 4 , զ 3 )

1) կողերի երկարությունը AB;.

2) անկյունը կողերի միջև ԱԲԵվ ԱԴ;

3) անկյունը եզրերի միջև ՀԱՅՏԱՐԱՐՈՒԹՅՈՒՆ և եզր ABC;

4) դեմքի տարածքը ABC;

5) բուրգի ծավալը.

6) ուղիղ գծի հավասարում ԱԲ;

7) հարթության հավասարումը ABC;

8) վերևից իջեցված բարձրության հավասարումը Դեզրին ABC.

n

x 1

y 1

զ 1

x 2

y 2

զ 2

x 3

y 3

զ 3

x 4

y 4

զ 4

Առաջադրանք 7.

Առաջադրանք 8. Գտե՛ք ֆունկցիայի տիրույթը

5.

7.

8.

9.

10.

Առաջադրանք 9. Գծապատկերե՛ք ֆունկցիան

1.

2.

3.

4

5.

6.

7.

8.

9.

10.

Առաջադրանք 10. Գտե՛ք ֆունկցիայի սահմանները

1.ա)
, բ)
, V)
,

է)
, ե)

2.ա)
, բ)
, V)
,

է)
, ե)

3.ա)
, բ)
, V)
,

է)
, ե)

4. ա)
, բ)
, V)
,

է)
, ե)

5.ա)
, բ)
, V)
,

է)
, ե)

6.ա)
, բ)
, V)
,

է)
, ե)

7. ա)
, բ)
, V)
,

է)
, ե)

8.ա)
, բ)
, V)
,

է)
, ե)

9.ա)
, բ)
, V)
,

է)
, ե)

10.ա)
, բ)
, V)
,

է)
, ե)

Առաջադրանք 11. Գտիր ածանցյալը

1.
, բ),

V)
, Գ)
, ե)
, ե)

2. ա)
, բ)
, V)
,

է)
, ե)
,ե)

3. ա), բ)
, V)
, Գ)
, ե)
, ե)

4. ա)
, բ)
, V)
,

է)
, ե)
, ե)

5. ա)
, բ)
, V)
, Գ)
, ե)
,

ե)

6. ա)
, բ)
, V)
, Գ)
, ե)
,

ե)

7. ա)
, բ),

V)
, Գ)
, ե)
,

ե)

8. ա)
, բ)
, V)
, Գ)
, ե)
,

ե)

9. ա)
, բ)
, V)
,

է)
, ե)
, ե)

10. ա)
, բ)
, V)
,

է)
, ե)
, ե)

Առաջադրանք 12. Ցույց տվեք, որ ֆունկցիան բավարարում է հավասարությանը

Առաջադրանք 13. Գտե՛ք պարամետրականորեն տրված ֆունկցիայի երկրորդ ածանցյալը:

1 .
6.

2.
7

3.
8

4.
9.

5.
10.

Առաջադրանք 14. Գտեք սահմաններ՝ օգտագործելով L'Hospital-ի կանոնը

Առաջադրանք 15. Գտե՛ք տրված ֆունկցիաների ծայրահեղությունները:

1.
6.

2.
7.

3.
8.

4.
9.

5.
10.

Առաջադրանք 16. Նշված հատվածների վրա և նշված ընդմիջումներով գտե՛ք ամենամեծ և ամենափոքր արժեքը:

Առաջադրանք 17. Կատարել այս ֆունկցիաների ամբողջական ուսումնասիրություն և նկարել դրանց գրաֆիկները:

1.
6.

2.
7.

3.
8.

4.
9.

5.
10.

Գրականություն:

Բավրին Ի.Ի. Բարձրագույն մաթեմատիկայի դասընթաց.-Մ.: Լուսավորություն, 1992.-400 էջ.

Բրոնշտեյն Ի.Ն., Սեմենդյաև Կ.Ա. Մաթեմատիկայի ձեռնարկ. M, 1967, 608 s

Բարձրագույն մաթեմատիկայի ընդհանուր դասընթաց տնտեսագետների համար, խմբագրությամբ Վ.Ի.Էրմակով-Մ. «Ինֆրա-Մ». 1999 - 655 էջ.

Թեուշ Վ.Լ. Բարձրագույն մաթեմատիկայի դասընթաց. - Մ.: Սովետական ​​գիտություն, 1958, 270 էջ.

Շիպաչով Վ.Ս. Բարձրագույն մաթեմատիկա. Ուսուցողական M. Բարձրագույն դպրոց, 1990.-479s.

Բարձրագույն մաթեմատիկա տնտեսագետների համար. Դասագիրք ավագ դպրոցների համար / Ն.Շ.Կրեմեր, Բ.Ա.Պուտկո և այլք; M: UNITI, 2002. - 461 p.

Վալև Կ.Գ., Ջալլադովա Ի.Ա. Օգնական.

Լուծումը կարելի է հեշտությամբ բաժանել երկու մասի.

1) Նախ ստուգում ենք՝ արդյոք կան ուղղահայաց ասիմպտոտներ։ Հայտարարը անհետանում է ժամը, և անմիջապես պարզ է դառնում, որ այս պահին ֆունկցիան կրում է անսահման ընդհատում, և հավասարման կողմից տրված ուղիղ գիծը ֆունկցիայի գրաֆիկի ուղղահայաց ասիմպտոտն է։ Բայց նման եզրակացություն անելուց առաջ անհրաժեշտ է գտնել միակողմանի սահմաններ.

Հիշեցնում եմ ձեզ հաշվարկման տեխնիկան, որը ես նմանապես քննարկել եմ ֆունկցիայի շարունակականություն հոդվածում։ Ընդմիջման կետեր. Սահմանի նշանի տակ արտահայտության մեջ «x»-ի փոխարեն փոխարինում ենք. Համարիչում հետաքրքիր բան չկա.

Բայց հայտարարում ստացվում է անսահման փոքր բացասական թիվ.

Այն որոշում է սահմանի ճակատագիրը:

Ձախ կողմի սահմանը անսահման է, և, սկզբունքորեն, արդեն հնարավոր է դատավճիռ կայացնել ուղղահայաց ասիմպտոտի առկայության վերաբերյալ: Բայց միակողմանի սահմաններ են անհրաժեշտ ոչ միայն դրա համար. դրանք ՕԳՆՈՒՄ ԵՆ ՀԱՍԿԱՆԵԼ, ԻՆՉՊԵՍ է գտնվում ֆունկցիայի գրաֆիկը և ճիշտ կառուցել այն: Հետևաբար, մենք պետք է նաև հաշվարկենք աջակողմյան սահմանը.

Եզրակացություն. միակողմանի սահմաններն անսահման են, ինչը նշանակում է, որ ուղիղ գիծը ֆունկցիայի գրաֆիկի ուղղահայաց ասիմպտոտն է:

Առաջին սահմանը վերջավոր է, ինչը նշանակում է, որ անհրաժեշտ է «շարունակել զրույցը» և գտնել երկրորդ սահմանը.

Երկրորդ սահմանը նույնպես վերջավոր է։

Այսպիսով, մեր ասիմպտոտը հետևյալն է.

Եզրակացություն. հավասարմամբ տրված ուղիղ գիծը ֆունկցիայի գրաֆիկի հորիզոնական ասիմպտոտն է:

Հորիզոնական ասիմպտոտը գտնելու համար կարող եք օգտագործել պարզեցված բանաձև.

Եթե ​​կա վերջավոր սահման, ապա տողը հանդիսանում է ֆունկցիայի գրաֆիկի հորիզոնական ասիմպտոտ:

Հեշտ է տեսնել, որ ֆունկցիայի համարիչն ու հայտարարը աճի նույն կարգի են, ինչը նշանակում է, որ ցանկալի սահմանը կլինի վերջավոր.

Ըստ պայմանի, անհրաժեշտ չէ ավարտել գծագիրը, բայց եթե ֆունկցիայի ուսումնասիրությունը եռում է, ապա մենք անմիջապես ուրվագիծ ենք կազմում սևագրի վրա.

Գտնված երեք սահմանների հիման վրա փորձեք ինքնուրույն պարզել, թե ինչպես կարող է տեղակայվել ֆունկցիայի գրաֆիկը: Բավական դժվար? Գտե՛ք 5-6-7-8 կետերը և նշե՛ք գծագրության վրա։ Այնուամենայնիվ, այս ֆունկցիայի գրաֆիկը կառուցված է տարրական ֆունկցիայի գրաֆիկի փոխակերպումների միջոցով, և ընթերցողները, ովքեր ուշադիր ուսումնասիրել են այս հոդվածի օրինակ 21-ը, հեշտությամբ կկռահեն, թե դա ինչ կորի է:

Սա «ինքներդ արա» օրինակ է: Գործընթացը, հիշեցնում եմ ձեզ, հարմար կերպով բաժանվում է երկու կետի՝ ուղղահայաց ասիմպտոտների և թեք ասիմպտոտների: Նմուշի լուծույթում հորիզոնական ասիմպտոտը հայտնաբերվում է պարզեցված սխեմայի միջոցով:

Գործնականում ամենից հաճախ հանդիպում են կոտորակային-ռացիոնալ ֆունկցիաներ, և հիպերբոլաների վրա մարզվելուց հետո մենք կբարդացնենք խնդիրը.

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

Լուծում. Մեկ, երկու և արված.

1) Ուղղահայաց ասիմպտոտները գտնվում են անսահման ընդհատման կետերում, ուստի մենք պետք է ստուգենք, թե արդյոք հայտարարը անհետանում է: Մենք կորոշենք քառակուսի հավասարում:

Խտրականը դրական է, ուստի հավասարումն ունի երկու իրական արմատ, և ավելացված է շատ աշխատանք

Միակողմանի սահմանները հետագայում գտնելու համար հարմար է քառակուսի եռանկյունը ֆակտորիզացնել.

(կոմպակտ նշման համար «մինուսը» ներկայացվել է առաջին փակագծում): Անվտանգության ցանցի համար մենք ստուգում կկատարենք մտովի կամ ցամաքի վրա՝ բացելով փակագծերը։

Եկեք վերագրենք ֆունկցիան ձևով

Գտեք միակողմանի սահմանները մի կետում.

ասիմպտոտային գրաֆիկի ֆունկցիայի սահմանը

Եվ կետում.

Այսպիսով, ուղիղ գծերը դիտարկվող ֆունկցիայի գրաֆիկի ուղղահայաց ասիմպտոտներն են։

2) Եթե նայեք ֆունկցիան, ապա միանգամայն ակնհայտ է, որ սահմանը վերջնական է լինելու, և մենք ունենք հորիզոնական ասիմպտոտ: Եկեք դա ցույց տանք կարճ ձևով.

Այսպիսով, ուղիղ գիծը (abscissa) այս ֆունկցիայի գրաֆիկի հորիզոնական ասիմպտոտն է։

Գտնված սահմանները և ասիմպտոտները շատ տեղեկություններ են տալիս ֆունկցիայի գրաֆիկի մասին։ Փորձեք մտովի պատկերացնել գծանկարը՝ հաշվի առնելով հետևյալ փաստերը.

Սևագրի վրա ուրվագծեք գրաֆիկի ձեր տարբերակը:

Իհարկե, հայտնաբերված սահմանները միանշանակ չեն որոշում գրաֆիկի տեսակը, և դուք կարող եք սխալվել, բայց վարժությունն ինքնին անգնահատելի օգնություն կլինի ֆունկցիայի ամբողջական ուսումնասիրության ընթացքում: Ճիշտ նկարը դասի վերջում է:

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

Սրանք անկախ որոշման առաջադրանքներ են։ Երկու գրաֆիկներն էլ ունեն հորիզոնական ասիմպտոտներ, որոնք անմիջապես հայտնաբերվում են հետևյալ հատկանիշներով. Օրինակ 4-ում հայտարարը մեծանում է համարիչից մեծ մեծության կարգով, իսկ օրինակ 5-ում համարիչն ու հայտարարը աճի նույն կարգի են: Նմուշի լուծույթում առաջին ֆունկցիան ամբողջությամբ ուսումնասիրվում է թեք ասիմպտոտների առկայության համար, իսկ երկրորդը՝ սահմանի միջով:

Հորիզոնական ասիմպտոտները, իմ սուբյեկտիվ տպավորությամբ, նկատելիորեն ավելի տարածված են, քան «իսկապես թեքվածները»: Երկար սպասված ընդհանուր դեպք.

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

Լուծում՝ ժանրի դասական.

• 1) Քանի որ հայտարարը դրական է, ֆունկցիան ամբողջ թվային տողի վրա շարունակական է, և ուղղահայաց ասիմպտոտներ չկան: …Լավ է? Ճիշտ բառ չէ՝ հիանալի: Թիվ 1 կետը փակ է:
• 2) Ստուգեք թեք ասիմպտոտների առկայությունը.

Երկրորդ սահմանը նույնպես վերջավոր է, հետևաբար, դիտարկվող ֆունկցիայի գրաֆիկն ունի թեք ասիմպտոտ.

Այսպիսով, ժամը , ֆունկցիայի գրաֆիկը անսահման մոտ է ուղիղ գծին:

Նկատի ունեցեք, որ այն հատում է իր թեք ասիմպտոտը սկզբում, և նման հատման կետերը միանգամայն ընդունելի են. կարևոր է, որ «ամեն ինչ նորմալ է» անսահմանության մեջ (իրականում հենց այնտեղ է առաջանում ասիմպտոտների քննարկումը):

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

Լուծում. մեկնաբանելու շատ բան չկա, ուստի ես կկազմեմ վերջնական լուծման մոտավոր նմուշ.

1) Ուղղահայաց ասիմպտոտներ. Եկեք ուսումնասիրենք կետը:

Ուղիղ գիծը սյուժեի ուղղահայաց ասիմպտոտն է ժամը:

2) թեք ասիմպտոտներ.

Ուղիղ գիծը սյուժեի թեք ասիմպտոտն է ժամը.

Գտնված միակողմանի սահմանները և ասիմպտոտները մեզ թույլ են տալիս բարձր հստակությամբ ենթադրել, թե ինչպիսին է այս ֆունկցիայի գրաֆիկը:

Գտեք ֆունկցիայի գրաֆիկի ասիմպտոտները

Սա անկախ լուծման օրինակ է, որոշ սահմաններ հաշվարկելու հարմարության համար կարող եք համարիչը բաժանել հայտարարի անդամով: Եվ կրկին, վերլուծելով արդյունքները, փորձեք նկարել այս ֆունկցիայի գրաֆիկը։

Ակնհայտ է, որ «իրական» թեք ասիմպտոտների տերերը այն կոտորակային-ռացիոնալ ֆունկցիաների գրաֆիկներն են, որոնց համարիչի ամենաբարձր աստիճանը մեկով մեծ է հայտարարի ամենաբարձր աստիճանից։ Եթե ​​ավելին - չի լինի թեք ասիմպտոտ (օրինակ,):

Բայց կյանքում լինում են նաև այլ հրաշքներ։